Lambda

Lambda演算是Alonzo Church在1930年代开发的框架，用于研究具有函数的计算。

• Function creation     - 教会引入了符号λx.E表示一个函数，其中" x"是形式参数，而" E"是函数身体，这些函数可以不带名称和单个参数。

• Function application- 教会使用符号 E 1 .E 2 表示应用程序函数 E 1 到实际参数 E 2 的作用，而且所有函数都在单个参数上。

微积分的语法

E::= x (变量)

| E 1 E 2 (函数应用)

| λx.E(函数创建)

其中λx.E被称为Lambda抽象，而E被称为λ表达式。

判断微积分

纯lambda演算没有内置函数，让我们判断以下表达式-

(+ (* 5 6) (* 8 3)) 

在这里，我们不能以" +"开头，因为它仅对数字起作用。有两个可简化表达式:(* 5 6)和(* 8 3)。

我们可以先减少一个。如-

(+ (* 5 6) (* 8 3)) 
(+ 30 (* 8 3)) 
(+ 30 24) 
= 54

β-reduction法则

我们需要一个简化规则来处理λs

(λx . * 2 x) 4 
(* 2 4) 
= 8

这称为β-reduction。

形式参数可以多次使用-

(λx . + x x) 4 
(+ 4 4) 
= 8

当有多个术语时，我们可以按以下方式处理它们-

(λx . (λx . + (- x 1)) x 3) 9 

内部 x 属于内部λ，外部x属于外部λ。

(λx . + (- x 1)) 9 3 
+ (- 9 1) 3 
+ 8 3 
= 11

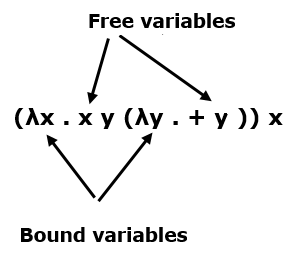
自由和绑定变量

在表达式中，变量的每个出现都是"free"(对λ)或"bound"(对λ)。

(λx。E) y的β还原将 E 中自由出现的每个 x 替换为 y 。如-

Alpha-Reduction

Alpha Reduction非常简单，无需更改lambda表达式的含义即可完成。

λx . (λx . x) (+ 1 x) ↔ α λx . (λy . y) (+ 1 x) 

如-

(λx . (λx . + (- x 1)) x 3) 9 
(λx . (λy . + (- y 1)) x 3) 9 
(λy . + (- y 1)) 9 3 
+ (- 9 1) 3 
+ 8 3 
11