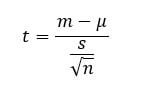T-teszt az R programozásban: egy minta és páros T-teszt [Példa]
Mi az a statisztikai következtetés?
A statisztikai következtetés az adatok eloszlására vonatkozó következtetések levonásának művészete. Az adattudós gyakran olyan kérdések elé kerül, amelyekre csak tudományosan lehet válaszolni. Ezért a statisztikai következtetés egy olyan stratégia, amely megvizsgálja, hogy egy hipotézis igaz-e, azaz érvényes-e az adatokkal.
A hipotézis értékelésének általános stratégiája a t-próba végrehajtása. A t-próba meg tudja mondani, hogy két csoport átlaga megegyezik-e. A t-próbát a Diák teszt. A t-próba a következőkre becsülhető:
- Egyetlen vektor (azaz egymintás t-teszt)
- Két vektor ugyanabból a mintacsoportból (azaz páros t-próba).
Feltételezi, hogy mindkét vektor véletlenszerűen mintavételezett, független, és egy normális eloszlású, ismeretlen, de egyenlő varianciájú populációból származik.
Mi az a T-teszt az R programozásban?
A T-teszt mögött meghúzódó alapötlet az, hogy statisztikákat használjunk két ellentétes hipotézis értékelésére:
- H0: NULL hipotézis: Az átlag megegyezik a használt mintával
- H3: Igaz hipotézis: Az átlag eltér a használt mintától
A T-tesztet általában kis mintaméreteknél használják. A t-próba végrehajtásához feltételezni kell az adatok normalitását.
T-Test szintaxis az R-ben
A t.test() alapvető szintaxisa R-ben:
t.test(x, y = NULL,
mu = 0, var.equal = FALSE)
arguments:
- x : A vector to compute the one-sample t-test
- y: A second vector to compute the two sample t-test
- mu: Mean of the population- var.equal: Specify if the variance of the two vectors are equal. By default, set to `FALSE`
Egy minta T-teszt R-ben
A One Sample t-próba vagy a Student-féle teszt egy vektor átlagát hasonlítja össze egy elméleti átlaggal, . A t-próba kiszámításához használt képlet a következő:
Itt,
az átlagra utal
az elméleti átlaghoz
- s a szórás
- n a megfigyelések száma.
A t-próba statisztikai szignifikanciájának értékeléséhez ki kell számítani a p-érték Az p-érték 0 és 1 között van, és a következőképpen értelmezhető:
- A 0.05-nél kisebb p-érték azt jelenti, hogy erősen biztos abban, hogy elutasítja a nullhipotézist, így a H3 elfogadott.
- A 0.05-nél nagyobb p-érték azt jelzi, hogy nincs elegendő bizonyíték a nullhipotézis elutasításához.
A p-értéket úgy állíthatja össze, hogy megnézi a Student-eloszlásban a t-próba megfelelő abszolút értékét, amelynek szabadságfoka egyenlő
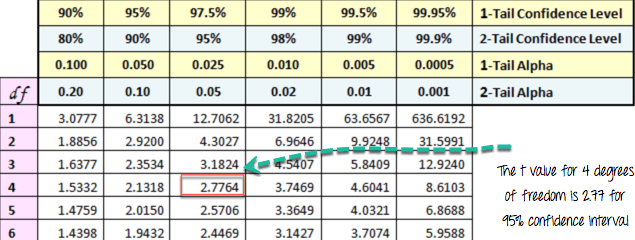
Például, ha 5 megfigyelése van, össze kell hasonlítania a t-értékünket a Student-eloszlás t-értékével, 4 szabadságfokkal és 95 százalékos konfidencia-intervallum mellett. A nullhipotézis elutasításához a t-értéknek nagyobbnak kell lennie, mint 2.77.
Lásd az alábbi táblázatot:
Egy minta T-teszt példa az R-ben
Tegyük fel, hogy Ön egy cookie-kat gyártó cég. Minden sütinek 10 gramm cukrot kell tartalmaznia. A sütiket egy gép állítja elő, amely egy tálban hozzáadja a cukrot, mielőtt mindent összekever. Úgy gondolja, hogy a gép nem ad hozzá 10 gramm cukrot minden sütihez. Ha a feltevés igaz, a gépet meg kell javítani. Harminc keksz cukorszintjét tárolta el.
Megjegyzések: Az rnorm() függvénnyel véletlenszerű vektort hozhatunk létre. Ez a függvény normál eloszlású értékeket generál. Az alap szintaxis a következő:
rnorm(n, mean, sd) arguments - n: Number of observations to generate - mean: The mean of the distribution. Optional - sd: The standard deviation of the distribution. Optional
Létrehozhat egy eloszlást 30 megfigyeléssel, 9.99-es átlaggal és 0.04-es szórással.
set.seed(123) sugar_cookie <- rnorm(30, mean = 9.99, sd = 0.04) head(sugar_cookie)
output:
## [1] 9.967581 9.980793 10.052348 9.992820 9.995172 10.058603
Egymintás t-próbával ellenőrizheti, hogy a cukorszint eltér-e a receptben megadottól. Felállíthat egy hipotézis tesztet:
- H0: Az átlagos cukorszint 10
- H3: Az átlagos cukorszint eltér 10-től
0.05-ös szignifikanciaszintet használ.
# H0 : mu = 10 t.test(sugar_cookie, mu = 10)
Itt van a kimenet:
Az egymintás t-próba p-értéke 0.1079 és 0.05 feletti. 95%-ban biztos lehet benne, hogy a gép által hozzáadott cukor mennyisége 9.973 és 10.002 gramm között van. Nem utasíthatja el a null (H0) hipotézist. Nincs elég bizonyíték arra, hogy a gép által hozzáadott cukor mennyisége nem követi a receptet.
Párosított T-teszt R-ben
A páros T-próbát vagy a függő minta t-próbáját akkor használják, ha a kezelt csoport átlagát kétszer számítják ki. A páros t-próba alapvető alkalmazása:
- A / B tesztelés: Hasonlítson össze két változatot
- Esettanulmányok: Kezelés előtt/után
Párosított T-teszt példa az R-ben
Egy italgyártó cég érdeklődik egy akciós program teljesítményéről az eladásokon. A cég úgy döntött, hogy követi az egyik üzletének napi eladásait, ahol a programot népszerűsítik. A program végén a cég azt szeretné tudni, hogy van-e statisztikai különbség az üzlet program előtti és utáni átlagos eladásai között.
- A cég a program indulása előtt minden nap nyomon követte az eladásokat. Ez az első vektorunk.
- A programot egy hétig reklámozzák, és minden nap rögzítik az eladásokat. Ez a második vektorunk.
- Végezze el a t-tesztet, hogy megítélje a program hatékonyságát. Ezt páros t-tesztnek nevezzük, mivel mindkét vektor értéke ugyanabból az eloszlásból származik (azaz ugyanabból a boltból).
A hipotézis tesztelése a következő:
- H0: Nincs különbség az átlagban
- H3: A két eszköz különbözik
Ne feledje, hogy a t-próba egyik feltételezése egy ismeretlen, de egyenlő szórás. A valóságban az adatok alig rendelkeznek egyenlő átlaggal, és ez a t-próba helytelen eredményéhez vezet.
Az egyenlő variancia-feltevés enyhítésére az egyik megoldás a Welch-teszt használata. R feltételezi, hogy a két eltérés alapértelmezés szerint nem egyenlő. Az adatkészletben mindkét vektor azonos szórással rendelkezik, beállíthatja a var.equal= TRUE értéket.
Létrehozunk két véletlenszerű vektort egy Gauss-eloszlásból, amelyek magasabb átlagértékkel rendelkeznek a program utáni eladásokhoz.
set.seed(123) # sales before the program sales_before <- rnorm(7, mean = 50000, sd = 50) # sales after the program.This has higher mean sales_after <- rnorm(7, mean = 50075, sd = 50) # draw the distribution t.test(sales_before, sales_after,var.equal = TRUE)
0.04606 p-értéket kapott, ami alacsonyabb, mint a 0.05-ös küszöb. Arra a következtetésre jut, hogy a két csoport átlaga jelentősen eltér. A program javítja az üzletek eladásait.
Összegzésként
- A statisztikai következtetés az adatok eloszlására vonatkozó következtetések levonásának művészete.
- A T-teszt a következtetési statisztikák családjába tartozik. Általában arra használják, hogy megtudják, van-e statisztikai különbség két csoport átlaga között.
- A One Sample t-teszt vagy a Student-féle teszt egy vektor átlagát hasonlítja össze az elméleti átlaggal.
- A páros T-próbát vagy a függő minta t-próbáját akkor használják, ha a kezelt csoport átlagát kétszer számítják ki.
A t-próbát az alábbi táblázatban foglalhatjuk össze:
| Tesztelés | Tesztelendő hipotézis | p-érték | Kód | Opcionális érv |
|---|---|---|---|---|
| egymintás t-próba | Egy vektor átlaga eltér az elméleti átlagtól | 0.05 |
t.test(x, mu = mean) |
|
| páros minta t-próba | Az A átlag különbözik ugyanannak a csoportnak a B átlagától | 0.06 |
t.test(A,B, mu = mean) |
var.equal= TRUE |
Ha feltételezzük, hogy az eltérések egyenlőek, akkor módosítanunk kell a var.equal= TRUE paramétert.