2025-05-27

西浦氏の Scientific Reports 論文について（１１）開示されたプログラムの問題点

西浦氏の Scientific Reports 論文について（７）「ワクチンで感染者が９割減」は誤りはこちらに。
https://sarkov28.hatenablog.com/entry/2024/12/17/184600

「接触8割減」の問題をまとめた論考はこちらに。
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

私がネット上でしていることのまとめはこちらに。
https://sarkov28.hatenablog.com/entry/2022/03/29/160915

（１）序論
（２）Google Colab で動作する改変プログラム
（３）開示プログラムは、論文の Figure S5 を再現しない
（４）デルタ株比率の最適化計算のコスト関数は不適切
（５）デルタ株比率推定の初期値設定が不適切
（６）結果
（７）考察
（付録Ａ）デルタ株に関する2つの概念
（付録Ｂ）プログラムＡ移動部分の動作確認
（付録Ｃ）高精度パラメータが必要な理由
（付録Ｄ）計算環境の検証
（付録Ｅ）局所極小の実態
更新履歴

（１）序論

西浦氏らのグループは、2023-10 に Scientific Reports にコロナワクチンに関する論文 [Kayano 2023] を発表しました。
これは後に共同通信が「コロナワクチンで死者9割以上減京都大チームが推計」と報じた論文です。（以下では [Kayano 2023] を Sci Rep 2023 論文、と書きます。）
Evaluating the COVID-19 vaccination program in Japan, 2021 using the counterfactual reproduction number
https://doi.org/10.1038/s41598-023-44942-6

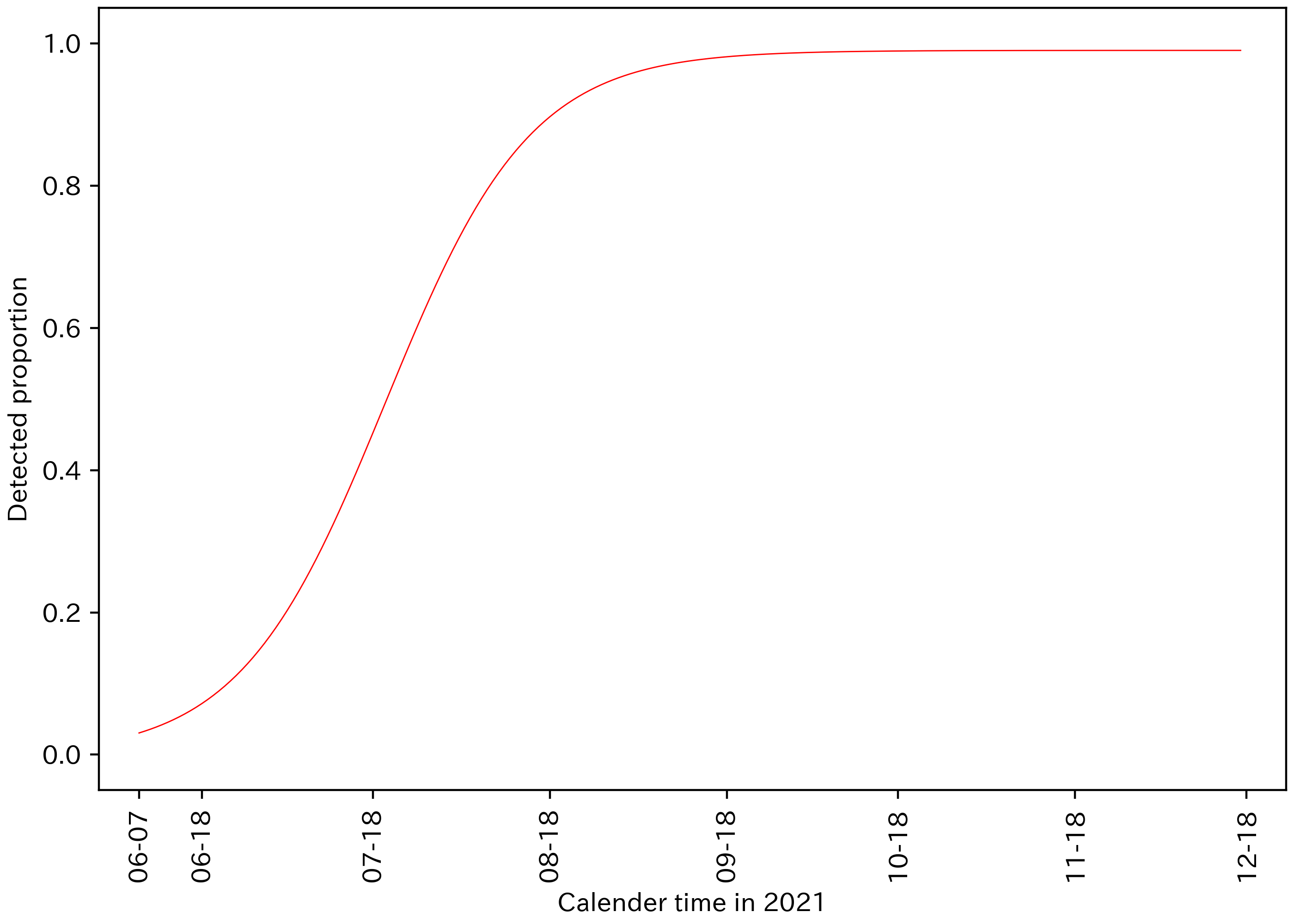
Sci Rep 2023 論文は、補足情報の Figure S5 に、白丸でデルタ株比率の観測値を示し、赤線でそれをモデル化しています。論文はこの赤線を、最大値が 1 のロジスティック曲線だと説明しています。図1.1 が論文の Figure S5 です。

図1.1　Sci Rep 2023 論文補足情報 Figure S5

最近（2025-04-19）になって西浦氏は、この論文の（HER-SYS データを除く）データと、計算に用いたプログラムを Zenodo で開示しました。プログラムは Evaluating the COVID-19 vaccination programs in Japan 2021_shared code_04112025.R です。本稿は、このプログラムの検証を行います。以後このプログラムを開示プログラムと呼びます [注1a]。HER-SYS データが示されていないので、開示プログラムの主要部分は動きません。しかしある程度は動かすことができます。

私は開示プログラムを改変し、Google Colab 上で動作するプログラムを作成しました。改変の内容については（２）節で説明します。（３）節では、開示プログラムが論文の Figure S5 を再現しないことを示します。（４）節では、デルタ株比率の最適化計算のコスト関数に不適切なところがあることを述べます。（５）節では、デルタ株比率の最適化計算における初期値の決定方法が不適切であることを述べます。（６）節では結果を述べ、（７）節では考察を述べます。

[注1a] 本稿では可搬性を考慮し、開示プログラムのファイル名を Evaluating the COVID-19 vaccination programs in Japan 2021_shared code_04112025.R と表記します。Zenodo で公開されているファイルでは COVID-19 のハイフンが見た目が似た別の文字になっていますが、ここでは通常のハイフンに置き換えました。（Zenodo 版は Unicode で U+2011、本稿が使う ASCII のハイフンは U+002D。）

（２）Google Colab で動作する改変プログラム

(2-1) 作成したプログラムの内容

私は、Zenodo で開示された R言語のプログラムを改変し、2つのプログラムを作成しました。

プログラムＡ（基準版）
開示プログラムに検証のための必要最小限の修正をしたもの。
https://colab.research.google.com/drive/1M3FMaatdXp8kppEvuzKZnMme_svwbAFh?usp=drive_link
プログラムＢ（R 言語 4.0.0 版）
プログラムＡの一部を、R 言語 version 4.0.0 で動作するようにしたもの。
https://colab.research.google.com/drive/1LwZZY6JG9U1ugaY0AySOERECnos7GB_C?usp=drive_link

また、python でプログラムＣとプログラムＤを作成しました。これらはプログラムＡと同じ問題を計算したり、この記事に示したグラフを作成するためのものです。

プログラムＣ
各種の計算とグラフ描画のためのもの。
https://colab.research.google.com/drive/1ztMyYaFYr-Yz234ir2eOOf8Qmxd01QK4?usp=drive_link
プログラムＤ
図4.2 や図E.1 のためのもの。
https://colab.research.google.com/drive/1mcU_AFKKqI8JJM2bxtrY_ql0LWSb9eL9?usp=drive_link

(2-2) 開示プログラムからの必要最小限の改変

開示プログラムからプログラムＡ（基準版）への主な修正点は以下です。

(a) ライブラリをインストールする関数、install_libraries() を追加。
(b) install_libraries() を使ってライブラリ pacman をインストール。
(c) データの読み込み先を指定する default_data_dir を導入し、ファイル読み込みに使用。
(d) デルタ株比率に関する処理を HER-SYS データ読み込みの前に移動。
(e) デルタ株比率の数理モデルのパラメータ計算の結果 outcome_delta を画面に出力。
(f) の計算結果 new_delta_df_v2 をファイルに出力。

このうち、(d) が重要です。図 2.1 にその概要を示します。

開示プログラムでは、デルタ株比率に関する処理は、HER-SYS データの読み込みの後にあります。HER-SYS データの読み込みでプログラムは停止するため、このままではこの部分は計算されません。しかしこの計算は HER-SYS データや関連する処理に依存していなかったので、私はこの部分を HER-SYS データの読み込みの前に移動しました。具体的には、開示プログラムの 214行目から 286行目までを、155行目の前に移動しました。（以後、（･･･行目）と示すのは、開示プログラムにおける行数です。）

この移動により、デルタ株比率の数理モデルのパラメータ計算や u_t の算出が行えるようになりました。（ u_t については（付録Ａ）をご参照下さい。）

図2.1　修正(d) の改変の概要。左は開示プログラムで、デルタ株比率などを計算するブロック（オレンジ）が File2 の処理より後ろに配置されている。右は同ブロックを File2 の処理より前へ移動した改変後の構成を示す。

(2-3) プログラムＡ（基準版）が開示プログラムと同様に動作することの確認

(2-2)節に示した移動の後も、移動した部分（＝デルタ株比率に関する処理）は開示プログラムと同様に動作しています。移動による動作の変化はありません。

私は、移動した部分が開示プログラムと同様に動作していることを確認しました。例えば開示プログラム 217行目は

delta_df <- data.frame(delta_0)

ですが、この右辺にあるのはその直前に読み込んだ変数なので、移動しても問題なく動作します。同様の確認を、移動対象（214行目から 286行目まで）の各行に対して行いました。（確認の詳細を（付録Ｂ）に示しました。）

したがって合理的に考えて、プログラムＡ（基準版）の移動した部分は、開示プログラムと同様に動作しています。

（３）開示プログラムは、論文の Figure S5 を再現しない

(3-1) 再現失敗の実証

プログラムＡ（基準版）は、デルタ株比率のロジスティック曲線のパラメータを最適化計算で計算しています。プログラムＡは、初期値が (phi1, phi2, phi3) = (99, 45, 0.07) で収束値が (phi1, phi2, phi3) = (98.983709648339, 45.016562723587, 0.078734384848) になります [注3-1a]。このパラメータでグラフを作成しました。

図3.1　デルタ株比率のモデル曲線。開示プログラムと同じ計算によるパラメータから。

図3.1 は図1.1（論文 Figure S5）の赤線と一致する必要があるので、重ね合わせて確認しました。

図3.2　論文の Figure S5 と図3.1 との重ね合わせ

図3.2 の緑点線は、赤線に似ていますが一致しているとは言えません。

(2-3) 節で示したように、プログラムＡは開示プログラムと同一のアルゴリズムで動作しています。そのプログラムＡが白丸データから計算した緑点線は、論文補足情報の Figure S5 に示された赤線に近いものの、完全には一致せず（図3.2）、赤線を再現しませんでした [注3-1b]。

同一アルゴリズムであるプログラムＡが Figure S5 の赤線を再現しないため、開示プログラムも Figure S5 の赤線を再現しないと考えられます。したがって今回の開示は、論文を再現するものとして不十分です。

[注3-1a] パラメータに多くの桁数の有効数字を示している理由については、（付録Ｃ）をご参照下さい。
[注3-1b] 図3.2 で緑点線が赤線を再現しなかった理由が (phi1, phi2, phi3) の丸め誤差ではないことは別途確認しています。これらパラメータを有効数字3桁で四捨五入した値を使ったグラフは（数値的に完全一致しないものの）視覚的には図3.2 の緑点線と区別がつきませんでした。一方で図3.2 の緑点線と赤線には明らかに視覚的な差があります。

(3-2) 図3.2 の不一致が私の作図上の不手際ではないことの検証

図3.2 は不一致を示していますが、赤線と緑点線は似ています。この不一致が、画像を重ねた私の不手際によるものなのかを検証するため、以下の要領で図3.3 を作図しました。

論文 Figure S5 の赤線を再現する曲線を最適化計算で計算する。
論文の Figure S5 と得られた曲線とを、図3.2 と同じ手順で重ね合わせる。

最適化計算や、重ね合わせ手順に不手際があれば、この要領で得られる図3.3 には不一致が見られるはずです。

図3.3　最適化計算や重ね合わせ手順に不備があれば不一致になる図

図3.3 の赤線と緑点線は、視覚的には区別できません。最適化計算や重ね合わせ手順に、不手際はないと思われます [注3-2a]。

[注3-2a] 厳密に言うと、図3.3 の一致は最適化計算や重ね合わせ手順に不備がない可能性を完全に排除はしていません。例えば何らかの不備があっても、それを別の不備が相殺したために結果的に一致して見えている可能性を排除できないからです。しかしこのようなことが起こる可能性は一般にかなり小さいと考えられます。この可能性を含めて確認したい場合は、プログラムＣの "Figure3_3.png" の作図部分をご参照下さい。

(3-3) 計算環境への依存性について

(3-1)節で検討したのは、開示プログラムが論文のグラフを再現しないという問題です。本来こうした検討の際には、（使用言語の version などの）検証用の環境を論文の環境と一致させることが好ましいです。今回の開示情報には R 言語のバージョンに関する情報がないので、検証用の R 言語のバージョンを開示情報に合わせることはできませんでした。

しかし本稿が行った検証の計算は、西浦氏の開示プログラムの計算と一致していると考えられるので、その理由を（付録Ｄ）に述べました。なお（３）節以外で述べている問題には、R 言語のバージョンなどの計算環境との実質的な関係はありません。

（４）デルタ株比率の最適化計算のコスト関数は不適切

(4-1) コスト関数の問題点とその回避策

開示プログラムのデルタ株比率の最適化計算のコスト関数は以下です。

$\displaystyle \sum_{w=1}^{12} \log((expt_{w} - vac_{w})^{2}) 　......\ \ 式(1)$

ここでは週を表す変数であり、図1.1（論文 Figure S5）の各白丸の x軸の値に対応しています。 $expt_{w}$ はデルタ株比率の観測値です。 $vac_{w}$ はデルタ株比率のモデル値です。式(1) は、観測値とモデル値が近づくと低下するように構成されています。

ただし $\log(x)$ は、が 0 に近づくと図4.1 に示すように急速に減少し、 x=0 では負の無限大に発散します（以下、単に発散と略記）。

図4.1　 $y = \log(x)$ のグラフ。 $\log(0)$ は発散する。このグラフの左下は (x, y) = (0.000001, -13.8)。

したがって式(1) はいずれかので $expt_{w} - vac_{w} = 0$ になる場合（あるいは0に近づく場合）は有限な値を計算できなくなります。これは特殊な状況ではなく、 $\log$ 関数を使い、このような（引数が 0 に近づく）計算を行う場合は常に注意すべき問題です。特に今回の計算では、 $expt_{w} - vac_{w} = 0$ となるのは想定すべき事態です。最適化計算がこの状態を目指しているからです。

$\log(0)$ の問題を回避するのは難しいことではありません。例えば式(1) の末尾に正の $\epsilon$ を加えれば、 $\log$ 関数の引数がに近づくのを回避できます [注4-1a]。

$\displaystyle \sum_{w=1}^{12} \log((expt_{w} - vac_{w})^{2} + \epsilon),\ （\epsilon = 1e-12）　......\ \ 式(2)$

これはよく採られる回避策であり、特殊なものではありません。しかし開示プログラムはこうした対応を採っていません。開示プログラムのコスト関数式(1) はこの意味で不適切です。

本稿の検討では特記しない限り式(1) を使いました。可能な限り開示プログラムと同じ計算をするためです。しかし一部では $\log(0)$ の問題が発生し、式(2) を使ったこともあります。（この場合でも最終的な関数の評価値としては式(1) を使いました [注4-1b]。）

[注4-1a] $\epsilon$ として幾つを使うのが適切なのかは、ここでは検討しません。 1e-12 は、コスト関数に与える影響を小さくするものとして使用しています。また $\log(0)$ への対策としては他に、異なる関数を用いる方法もあります。
[注4-1b] この回避方法は万全ではありません。最終的な関数の評価値計算に式(1) が使用できない状況もあり得るからです。こうした状況があり得るので、式(1) のようなコスト関数を使うべきではないのです。

(4-2) コスト関数の断面の形状 ─ 最適化を誤誘導する仕組み

本節で示すグラフは、コスト関数の特徴的な形状を可視化したものです。

開示プログラムのコスト関数は (phi1, phi2, phi3) と開示情報の File5 から計算されます。File5 は所与のものと考えていいので、コスト関数は実質的に3パラメータです。本節ではコスト関数の特定の断面のグラフをプログラムＤを用いて計算します。

開示プログラムの初期値 (phi1, phi2, phi3) = (99, 45, 0.07) を基準としました。この周辺で、phi1 だけを変化させながらコスト関数値を計算し、横軸を phi1、縦軸をコスト関数値とするグラフを作成しました。図4.2 です。

図4.2　(phi2, phi3) = (45, 0.07) で phi1 を変化させた時のコスト関数値

図4.2 には12個の「局所極小」があります。これは、以下の状況があるからです。

(phi2, phi3) = (45, 0.07) に対して、各白丸を通過する phi1 が存在する。その (phi1, phi2, phi3) では、（通過する白丸に関する残差がなくなるために）コスト関数式(1) が $\log(0)$ を計算し、関数値が発散する。

図4.2 に12個の「局所極小」が見えているのは、上の状況が図1.1（論文 Figure S5）の12個の白丸それぞれで起きているからであることを、別途確認しています。（正確にはこれは局所極小ではなく、実質的な局所極小にすぎません。（付録Ｅ）をご参照ください。）

またこれら「局所極小」は、図4.2 に示したように形状が極端に狭く、中心に向かって勾配が急峻化しています。（この形状は、図4.1の左端の形状と密接に関連しています。）

つまりコスト関数式(1) は

無数の「局所極小」がある。
それぞれの「局所極小」の形状が極端に狭く、中心に向かって勾配が急峻化する。

という性質があります。このため最適化計算は、「局所極小」に収束しやすくなります。なお式(2) のように $\epsilon$ を加えればコスト関数値は発散しなくなり、比較不能になる問題は解消します。それでも $\epsilon$ が小さければ「局所極小」は残るので、最適化が初期値に強く依存することに変わりはありません。

(4-3) コスト関数が「適切」と示す曲線が白丸のモデルとして適切とは限らない

式(1) が示すように、また図4.2 が例示するように、開示プログラムのコスト関数は「計算されたパラメータによる曲線が一つの白丸の上を通過すれば、（他の白丸との位置と無関係に）関数値が発散する」との性質を持っています。

開示プログラムが使用しているロジスティック曲線の式は、式(3) です。

$\displaystyle y = phi1 / (1 + \exp(-phi3 \times (x - phi2))) 　......\ \ 式(3)$

式(3) を phi3 について解くと、式(4) になります。

$\displaystyle phi3 = - \log(phi1 / y - 1) / (x - phi2) 　......\ \ 式(4)$

したがって式(4) を満たす正の x, y, phi1, phi2 があれば (x, y) を通過する (phi1, phi2, phi3) を計算できます。

式(4) を使い、例として File5 の8番目の白丸、(x, y) = ('2021-07-26', 67) を通過する phi3 を (phi1, phi2) = (85, 35) で計算しました [注4-3a]。この曲線のコスト関数は発散します。こうして得られた (phi1, phi2, phi3) による曲線を描画し、論文の Figure S5 と重ね合わせたのが図4.3 です。

図4.3　(x, y) = ('2021-07-26', 67) を通過し、コスト関数が発散する曲線と、論文 Figure S5 との重ね合わせ

図4.3 の緑点線が白丸の列全体と乖離していることは一目で分かります。しかしこの緑点線は、('2021-07-26', 67) の白丸を通過しているためにコスト関数値は負の無限大に発散していて、数値的にはこの曲線を「最適」と示しています。この緑点線はコスト関数が不適切であることの端的な例です。開示プログラムのコスト関数の値は、「曲線の白丸のモデルとしての適切さ」を表現できていません。しかも上の計算方法から明らかなように、この緑点線と同様にコスト関数が「最適」と示す曲線は無数にあります [注4-3b]。

なお式(2) のように $\epsilon$ を加えるとこの曲線のコスト関数値は「最適」にはなりません。 $\epsilon$ のために発散しなくなり、他の白丸と緑点線との不一致によってこのコスト関数の値は（「局所極小」ではありますが、「局所極小」の値としては）小さめのものにならないからです [注4-3c]。

[注4-3a] 計算された phi3 の値は 0.08762139076632007 なので、描いた曲線のパラメータは (phi1, phi2, phi3) = (85, 35, 0.08762139076632007) です。この phi3 は（付録Ｃ）で例示した小数点以下12桁では精度が足りず、16桁の精度が必要です。16桁ならば式(1) は発散しますが、15桁では約-24.0 になります。 $\log(0)$ 付近の発散が起きるところでは高精度の数値が必要なのですが、この事例はこれに該当しています。
[注4-3b] 今回は (phi1, phi2) = (85, 35) で計算しましたが、他の (phi1, phi2)、例えば (81.2, 35) でも同様の計算を行うことができ、異なる曲線が得られ、その曲線のコスト関数値は発散します。
[注4-3c] 図4.3 の緑点線の式(2) の値は約12.1 であり、小さめとは言えません。例えば図3.1 の曲線の式(2) の値は約-13.4 です。

(4-4) コスト関数を改善する式(2) 以外の方法

開示プログラムのコスト関数式(1) を改善する一つの方法は、式(1) を式(2) のように修正することです。式(2) では $\epsilon = 1e-12$ を使いましたが、この値が最適とは限りません [注4-1a]。（付録Ｅ）では、別の $\epsilon$ の値について述べています。

コスト関数を改善する他の方法として、別のコスト関数の使用があります。別稿は Zenodo への情報開示の前に書いた記事ですが、ここではよく使われる別のコスト関数 $\sum (残差の二乗)$ を用いた場合について検討しています。

（５）デルタ株比率推定の初期値設定が不適切

（４）節では、開示プログラムのコスト関数が、「曲線の白丸のモデルとしての適切さ」を表現できていないと述べました。しかし本節では、この問題をとりあえず措き、開示プログラムの主張「より小さなコスト関数値の曲線が、より適切なモデルである」に沿って検討します。

(5-1) 単一初期値での最適化は不適切

論文は、デルタ株比率をロジスティック曲線でモデル化したと述べています。ロジスティック曲線のパラメータ (phi1, phi2, phi3) は、コスト関数 nll_func_delta を最小化して計算されています。（コスト関数は、ロジスティック曲線が白丸に近づくと低下するように構成されていますが、（４）節に述べた問題があります。数式は（４）節の式(1) を参照。）

開示プログラムの処理は、

単一の初期値による最適化計算の収束値を最終的な結果とする

との方法です（主に、開示プログラムの255行、256行）。一般論として、この方法でも（プログラム作成者が意図したであろうレベルの）適切な計算結果が得られる可能性がゼロとは言えません。しかし一般に（この問題のような非線形最適化問題では）異なる初期値から計算を開始すると、異なる収束値が得られることがあります。プログラム作成者は、少なくともそうなることを想定したプログラムを作成すべきです。これを想定した場合、

複数の（しばしば多数の）初期値による最適化計算の収束値を得て、その中からコスト関数の意味で最適なものを最終的な結果とする

などの対策を採ります。しかし開示プログラムはこうした対策を採っていません。特に、開示プログラムのコスト関数には、図4.2 が例示したように無数の「局所極小」があります。このようなコスト関数において単一の初期値から計算を開始すると、その計算は初期値に近い「局所極小」に収束する可能性が高いです。

これは論文の主たる計算に用いる重要なパラメータを求める計算であるのに、開示プログラムは結果が初期値に強く依存する設計になっています。開示プログラムの「単一の初期値による」との方法で (phi1, phi2, phi3) を計算するのは不適切です [注5-1a]。

[注5-1a] 多数の初期値から計算をするなどの対策を講じても、(phi1, phi2, phi3) の計算から偶然の要素（運の要素）を完全に排除することは一般にできません。ここで述べている「不適切」というのは、「問題を回避するために通常採られる対策を採っていない」という意味です。

(5-2) 別初期値でのコストの改善

(5-1)節では、開示プログラムが単一の初期値による収束値を最終的な結果としている問題を一般論として指摘しました。本節ではこの問題が（一般論ではなく）現実化している例を示します。

本節ではプログラムＣを使います。開示プログラムの単一の初期値は、(phi1, phi2, phi3) = (99, 45, 0.07) であり（255行目）、プログラムＡも同じ値を使っています。本節ではこれを以下のように変更しながら計算しました。

「phi1 を [98, 99, 100]、phi2 を [44, 45, 46]、phi3 を [0.06, 0.07, 0.08] と変化させながら初期値を作成し、この初期値から最適化計算を行う」という方法です。最初に作成される初期値は (98, 44, 0.06) であり、最後は (100, 46, 0.08) であり、合計で $3 \times 3 \times 3 = 27$ 個の初期値になります。

27個の中には開示プログラムの初期値 (99, 45, 0.07) が含まれていて、この場合の収束値はプログラムＡと（したがって開示プログラムと）同じものになります。

ここで採用しているのは、開示プログラムが用いた単一の初期値の周辺を探索する方法として、きわめて素朴なものです。これは、初期値決定の良い方法として示しているのではなく、むしろ開示プログラムのように単一の初期値を採用する前に、論文著者らが少なくともこのような探索を試みるべきだ、という例として示しています。

27個の初期値から計算し、結果を集計すると表5.1 になりました。

計算の特徴	計算回数	得られた解の個数	より適切な解の個数
開示プログラムと同じ計算ただし初期値を変更	`27`	`27 (100%)`	`11 (40.7%)`

表5.1 (5-2)節の 27個の初期値による計算結果の集計。「より適切」は「開示プログラムより式(1) の値が小さい」。

表5.1 に「得られた解の個数」という項目があるのは、初期値によっては解が求まらないことがあるからです。今回の場合、そうした事例はありませんでした。また全27回のうち 11回で、開示プログラムより小さなコスト関数値が得られました。

表5.1 で集計した 27個の初期値のうち、最小のコスト関数値になった初期値の計算を、開示プログラムの初期値の計算と比較したのが表5.2 です。

初期値の特徴	初期値	計算結果（収束値）	収束値のコスト関数値
(a) 開示プログラムの初期値	`(99, 45, 0.07)`	`(98.98, 45.02, 0.07873)`	`-13.4`
(b) 表5.1のうちコスト関数値最小の初期値	`(99, 46, 0.08)`	`(99.00, 46.00, 0.07721)`	`-31.0`

表5.2 開示プログラムの初期値による計算結果と、表5.1 のうちコスト関数値最小の計算結果の比較。初期値と収束値は (phi1, phi2, phi3)。収束値とコスト関数値は概数。収束値のより詳細な値については [注5-2a]。コスト関数値は小さいほど適切と見なす構成なので、開示プログラムよりも適切な計算結果が得られている。

(b) のコスト関数値は、プログラムＡのコスト関数値（約-13.4）よりも小さな値（約-31.0）になりました。これは、コスト関数の意味で開示プログラムより適切なパラメータを発見したことを意味します。(5-1)節で「「単一の初期値による」との方法で計算するのは不適切」と述べましたが、今回見つけた収束値はその指摘が妥当だったことの実例です。

ただしここで発見した収束値によるグラフと、開示プログラムの収束値によるグラフ（図3.1）とにおいて、どちらが白丸のモデルとして適切なのかは、視覚的にははっきりしません。図3.2 と同じ要領で重ね合わせを作成しました。図5.1 です。

図5.1　論文の Figure S5 と表5.2 (b) の収束値による曲線との重ね合わせ

[注5-2a] 表5.2 (a) の収束値の詳細は (3-1)節に。(b) の収束値の詳細は (99.001589540997, 45.997614933974, 0.077212061586) です。多くの桁数を示す理由は（付録Ｃ）をご参照下さい。

(5-3) 広範な初期値探索でのコストの大きな改善

(5-2)節では、初期値を素朴な方法で複数用意した結果を開示プログラムの方法と比較しました。本節で示すのはランダムな1000個の初期値による計算です。また、最適化アルゴリズムを開示プログラムが採用している BFGS 法から Nelder-Mead 法に変更しました。

プログラムＣを使いました。初期値はラテンハイパーキューブサンプリングによる1000個です。この計算をコスト関数式(1) を用いて行うと（４）節で述べた $\log(0)$ に関する問題が発生したので、コスト関数は式(2) を使いました。 1000個の結果を集計すると表5.3 になりました。

計算の特徴	計算回数	得られた解の個数	より適切な解の個数
開示プログラムから計算言語、最適化アルゴリズム、初期値を変更	`1000`	`870 (87.0%)`	`839 (83.9%)`

表5.3 1000個の初期値による計算結果の集計。「より適切」は「開示プログラムより式(1) の値が小さい」。

表5.3 で集計した 1000個の初期値のうち最小のコスト関数値になった計算を、開示プログラムの初期値の計算などと比較したのが表5.4 です。比較のため、表5.2 に追加する形で示します。

初期値の特徴	初期値	計算結果（収束値）	収束値のコスト関数値
(a) 開示プログラムの初期値	`(99, 45, 0.07)`	`(98.98, 45.02, 0.07873)`	`-13.4`
(b) 表5.1のうちコスト関数値最小の初期値	`(99, 46, 0.08)`	`(99.00, 46.00, 0.07721)`	`-31.0`
(c) 表5.3のうちコスト関数値最小の初期値	`(93.06, 42.41, 0.09895)`	`(94.53, 42.20, 0.1004)`	`-140.3`

表5.4 表5.3 のうちコスト関数値最小の計算結果。表5.2 に追加して示した。一部の結果は概数。より詳細な値については [注5-3a]。コスト関数値は小さいほど適切と見なす構成なので、(c) が最も適切な計算結果になる。

表5.4(c) の収束値によるグラフで、図3.2 と同じ要領で重ね合わせを作成したのが、図5.2 です。

図5.2　論文の Figure S5 と表5.4 (c) の収束値による曲線との重ね合わせ

図5.2 の緑点線は、視覚的にも赤線より白丸のモデルに適合しています。図5.2 の緑点線の存在は、(5-1)節に示した「「単一の初期値による」との方法で計算するのは不適切」との指摘の正しさを強く支えます。

なお本来なら、数理モデルの白丸への適合は、専らコスト関数で評価すべきです。ところがコスト関数には（４）節に述べた問題があるので、この関数の値だけを指標とすることには疑問があります。このため、（主観的になるので好ましくない）視覚的な判断が必要になっています。

[注5-3a] 表5.4 の (a)(b) の詳細については [注5-2a] をご参照ください。(c) のより詳細な初期値は (93.059492680469, 42.405480670085, 0.098950644407)、収束値は (94.530734183607, 42.198896016416, 0.100367830190) です。多くの桁数を示す理由は（付録Ｃ）に。

（６）結果

西浦氏は、Sci Rep 2023 論文に関連して Zenodo にプログラムとデータを開示しました。

開示されたプログラムは本来、論文の補足情報の Figure S5 の赤線のパラメータを再現するはずですが、（３）節で示したように、実際には再現しません。

さらにこのプログラムのコスト関数は、 x=0 になる可能性のある値に対して $\log(x)$ を計算しています。このコスト関数は負の無限大に発散する可能性があることを（４）節で述べました。この問題を回避する一般的な方法がありますが、開示されたプログラムはこの方法を採用していません。コスト関数の特定の断面を図4.2 に示し、コスト関数の形状に問題があることを確認しました。

また、白丸のモデルとして適切とは言えない曲線のコスト関数が負の無限大に発散する（＝適切だと評価する）例として図4.3 を示しました。この曲線は特別な例ではなく、同様の事例は無数にあります。つまりこのコスト関数は、「白丸のモデルの適切さを評価する」との目的を果たせていません。

（５）節では、開示されたプログラムが Figure S5 の赤線のパラメータを求める計算を、単一の初期値により行っている問題を検討しました。開示プログラムの初期値の周辺を素朴な方針で探索するだけでも、コスト関数の意味で優れた収束値が見つかることを表5.1、表5.2 に示しました。また、多数の初期値から計算を開始することでさらにコスト関数の意味で優れた収束値が見つかることを、表5.3、表5.4 に示しました。表5.4 (c) の曲線は、視覚的にも Figure S5 白丸によく適合します（図5.2）。また、問題のあるコスト関数ではありますが関数値を参考までに示しておくと、開示プログラムと同じロジックが示す収束値では約-13.4 である一方、表5.4(c) では約-140 です。

（７）考察

本稿で検討した問題の中でも重大で、かつ事実として明確なのは、「プログラムＡ（＝開示プログラムと同様に動作）が、論文のデルタ株比率 Figure S5 の赤線を再現しない」という点です。（３）節に示したこの問題は、単なる数値の不一致ではなく、論文に掲載された図が、開示されたプログラムとデータによって再現できないことを意味しています。この点において、開示されたプログラムは論文の計算を再現する情報開示ではありません。再現性は科学的検証の前提条件であり、これが実現していないため、論文の信頼性に重大な疑義が生じています。

開示プログラムのコスト関数には（４）節で示した問題があります。 $\sum \log(残差の二乗)$ は、残差ゼロ付近で数値的に不安定になります。一般には $\epsilon$ を加えるなどで安定化が図られるのですが、開示されたプログラムはこれを行っていません。これは実装ミスではなく、設計方針における選択の問題だと思われ、計算の安定性に対する配慮不足を示唆しています。この意味でこのコスト関数は不適切です。

さらに（５）節で検討した通り、このプログラムは重要なロジスティック曲線のパラメータ推定で、単一の初期値による最適化計算を行っています。これも設計方針における選択の問題であり、非線形最適化でよく用いられる方法と比較して、結果の信頼性を大きく損なうものと言えます。さらに、異なる初期値から開始した計算がより良いコスト関数値に収束することを示したので、この初期値に関する設計方針は、一般論としての問題ではなく、開示プログラムが解こうとしている課題における、具体的な問題につながっています。この意味でこの初期値の設定方法は不適切です。

論文が、こうした設計方針を正当化する説明を論文本文、補足情報、開示プログラムなどで十分に示していない点も問題です。単一の初期値で十分である、単一の初期値としては (99, 45, 0.07) が適切であると判断したなら、あるいはコスト関数の安定化が不要だと判断したなら、その理由を明示的に示す必要があります。明示的な説明がない以上、読み手はこれらが特段の理由なく判断されたと捉えざるを得ません。

西浦氏が Zenodo で開示したのは、論文の最終的な計算を行うものではなく、試作段階の小規模で不完全な計算を行うプログラムだった可能性もありますが、いずれにせよ西浦氏ら論文著者には、まず次の最重要の問題があること確認し、その理由を説明する責任があります。

開示したプログラムが、論文の Figure S5 の曲線を厳密に再現しないこと。

現状は、情報開示によって論文の再現性を担保するという科学的要件が満たされていません。

また西浦氏ら論文著者には、デルタ株比率の数理モデル計算に関して以下を説明する責任があります。

開示したプログラムが、 $\log(0)$ 付近で発散し得るコスト関数を採用した理由。
開示したプログラムが、最適化計算を単一の初期値で行っている理由。
開示したプログラムが、単一の初期値として他の値ではなく特に (99, 45, 0.07) を選択した根拠。
開示したプログラムが (99, 45, 0.07) 以外の初期値から計算を開始すれば、コスト関数の意味でより適切な数理モデルが得られる例があることの説明。

これらは、開示したプログラムが示している計算の妥当性を示すために必要です。

本稿は開示プログラムのうちデルタ株比率に関する部分のみを検証し、幾つかの問題を指摘しました。HER-SYS データがないため、感染者数推計など後続解析の再計算は行えていません。HER-SYS データが必要な計算部分についても、同様の検証を行う必要があります。

（付録Ａ）デルタ株に関する2つの概念

論文には、デルタ株に関する2つの概念があります。

1つ目の概念は「その時点で市中にあるデルタ株の比率」です。これは図1.1（論文 Figure S5）の縦軸であり、[0, 1] の範囲です。本稿ではこれを単に「デルタ株比率」と記述します。図1.1 の白丸がデルタ株比率の観測値であり、赤線がデルタ株比率のモデル値（＝数式で表現した値）です。

2つ目の概念は、論文が「その時点でのデルタ株による感染性増加のプロファイル」と説明している変数 u_t です。これは [1, 1.5] の範囲です。本稿ではこれを u_t と記述します。

u_t （＝2つ目）は、デルタ株比率のモデル値（＝1つ目のモデル値。図1.1 の赤線。）を変換して計算します。開示プログラムで u_t は、変数 new_delta_df_v2 に入ります（開示プログラム 280行目）。

（付録Ｂ）プログラムＡ移動部分の動作確認

箇条書きで示したのは、プログラムＡ（基準版）の移動部分が開示プログラムと同様に動作することの確認の一部です。(2-3)節に述べた事項の詳細です。

移動した行と、それぞれの動作が移動後も変わらない理由を述べています。

(a) 215行 delta_0 <- read.csv('.../File5.Delta_japan.csv')
この右辺はファイルからの読み込みです。
(b) 217行 delta_df <- data.frame(delta_0)
この右辺にあるのは (a) で読み込んだ変数です。
(c) 222行 delta_df2 <- delta_df %>% filter(Date <= as.Date("2021-08-23"))
この右辺にあるのは (b) で定義した変数と定数です。
(d) 224行 delta_duration <- as.numeric(max(delta_df2$Date) - min(delta_df2$Date)) + 1
この右辺にあるのは (c) で定義した変数です。
(e) 226行 obs_delta <- numeric(delta_duration)
この右辺にあるのは (d) で定義した変数です。

(a)～(e) の要領で開示プログラムの移動する部分の全て（214行目から 286行目まで）を検討し、これらを 155行目の前に移動しても動作が変わらないことを確認しました。移動する全ての行についての確認は、
https://docs.google.com/spreadsheets/d/1AdPOYo7mWRaJetWOdxmqJTXkgdk6RcuOZ4ZoFEcrtIM/edit?usp=sharing
をご参照下さい。

（付録Ｃ）高精度パラメータが必要な理由

[注3-1a]、[注5-2a]、[注5-3a] では、(phi1, phi2, phi3) の値として多くの桁数を示しています。多くの桁数が必要な理由は以下です。

この最適化計算の入力データ（File5 の、市中のデルタ株比率）の有効数字は高々2桁です。しかし特記のない限り本稿では、ロジスティック関数のパラメータを小数点以下の有効数字を12桁で示します。多くの桁数で示すのは、コスト関数の値がこれらパラメータの値に非常に敏感な場合があるためです。

例えばパラメータ phi3 が 1e-12 変化しただけで、コスト関数の値が約-140 から約-136 へと変化することがあります。こうしたことが起きるのは、この最適化計算に用いているコスト関数が $\sum \log(残差の二乗)$ の形であるため、残差が 0 に近づく付近でのコスト関数の傾きが極めて大きくなるからです。この敏感さは（４）節で述べているコスト関数の問題に密接に関わっています。グラフを視覚上区別できない程度に描くためならばこれほどの精度は必要ありません。高精度の数値が必要になるのは、曲線が目標データ（の一部）に接近した状況でコスト関数値を計算する場合です。[注4-3a] に挙げた例は特にこの場合に該当していて、16桁の精度が必要になっています。

（付録Ｄ）計算環境の検証

本記事で行った検証の計算が、西浦氏の計算環境における開示プログラムの計算と一致していると考える根拠を述べます。(3-3)節に述べた事項の詳細になります。

(a) 西浦氏が 2020-05 に github https://github.com/contactmodel/COVID19-Japan-Reff に示した R 言語のプログラムには、version 4.0.0 で動作した旨が明記されています。
(b) 私は、プログラムＢとして R 言語 version 4.0.0 の環境を作り、今回の開示プログラムのデルタ株比率に関する処理を動作させました。すると R 言語 version 4.5.0（＝検証に用いた R 言語）での動作と、計算結果が一致しました。（R 言語 version 4.2.2 でも結果は同様でした。）

論文が発表されのは、(a) のおよそ 3年半後ですから、論文の計算を行った R 言語は version 4.0.0 以降であろうと推測できます。その version 4.0.0 （や version 4.2.2）と検証に用いた version 4.5.0 が、開示プログラムのデルタ株比率に関する処理で同様に動いています。

よって本稿が用いた R 言語 version 4.5.0 での計算は、西浦氏の計算環境における開示プログラムの計算と一致していると考えることができます。

なお論文には、ライブラリ surveillance の version 1.20.3 を使ったとの記述があります。しかし surveillance version 1.20.3 に必要なのは R 言語本体 version 3.6.0 以降なので、surveillance の version 情報から R 言語本体の version を特定することはできません。

（付録Ｅ）局所極小の実態

(4-2)節の図4.2 では、コスト関数式(1) の断面の「局所極小」を示しました。正確に言うとこれは局所極小ではありません。

なぜなら図4.2 の「窪み」は、単独の窪みではなく、「窪みが繋がった谷」のような形状だからです。図E.1 は、phi3 = 0.07 を固定し、phi1 と phi2 を変化させた時のコスト関数の値です。図E.1 の断面が図4.2 です [注Ea]。（本来なら図E.1 には12本の谷が見えるはずですが、図で個々の谷は判別しにくくなっています。）

図E.1 phi3 = 0.07 で phi1, phi2 を変化させた時のコスト関数値

一方でこれらの「谷」は、最適化計算上は無数の局所極小のように見えます。

ある初期値から開始した最適化計算は「谷」の低いところを探すのですが、この際、必ずしも大局的に低い方向ではなく、現在地で判定した下降方向に向かいます。結果的に大局的に低いところに至る場合もありますが、図E.1 のコスト関数では、谷に入ってさらに狭い谷の下方を目指すため、狭いところで「動きが取れなくなって」停止します。この停止位置は計算開始位置に強く左右されるので、異なる初期値からは、ほぼ異なる収束値に至ります。したがって実質的に無数の局所極小があるかのように見えるのです。ここでコスト関数としてどうしても式(1) を用いる必要があるなら、最適化アルゴリズムの工夫を検討すべきでしょう。しかし「デルタ株比率の数理モデル化」に対処するために行うべきことは、コスト関数の改善だと思われます。

1e-2 や 1e-1 のように極端に大きな値の $\epsilon$ が効果的かも知れません。このような $\epsilon$ は、発散を回避するというより局所極小を埋めるためのものです。こうした $\epsilon$ でも数式上は各白丸に近い曲線への収束が期待されるところ、別途行った確認によると、実際に有望と思われる曲線が得られています。

[注Ea] 図E.1 の方が空間の分割が粗い上、図E.1 は scipy.ndimage.gaussian_filter(sigma=1, truncate=2.0) で処理しているので、コスト関数の値には違いがあります。

更新履歴

2025-05-27
公開。
2025-08-24
(4-4)節を追加。
2025-09-10
- 「（対策を）取る」という語を用いていた何ヵ所かを「採る」に修正しました。
- (3-2)節のタイトルに「私の」を追加して誤解を招かないようにしました。

2025-04-01

西浦氏の Scientific Reports 論文について（１０）論文 Figure S5 の妥当性への疑問

西浦氏の Scientific Reports 論文について（１１）開示されたプログラムの問題点はこちらに。
https://sarkov28.hatenablog.com/entry/2025/05/27/163000

「接触8割減」の問題をまとめた論考はこちらに。
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

私がネット上でしていることのまとめは、こちらに。
https://sarkov28.hatenablog.com/entry/2022/03/29/160915

（０）本稿公開後に示された、論文の開示情報について（その１）
（１）序論
（２）Figure S5 の赤線は最大値 1 のロジスティック曲線と説明されている
（３）Figure S5 の赤線の最大値は 1 ではない
（４）Figure S5 の赤線のパラメータの推定
（５）（４）節で推定した曲線と赤線の重ね合わせ（図5.2）
（６）Figure S5 の白丸に適合するロジスティック曲線のパラメータの推定
（７）（６）節で推定した曲線と白丸の重ね合わせ（図6.1）
（８）最小値0・最大値1に固定したロジスティック曲線による白丸への適合
（９）結果
（１０）考察
（１１）結論
（１２）本稿公開後に示された、論文の開示情報について（その２）
更新履歴

（０）本稿公開後に示された、論文の開示情報について（その１）

本稿を書いた後の 2025-04 に、本稿が検討している論文 [Kayano 2023] に関する情報を西浦氏が開示しました。

しかしこの開示情報は論文のグラフを（再現するはずなのに）再現しません。また論文のグラフは（開示情報のコスト関数の意味で）最適なグラフではありません。これらは開示情報や論文のグラフが期待されたものとは異なることを示しています。

私はこれらを含む論文や開示情報の問題を指摘する別稿「西浦氏の Scientific Reports 論文について（１１）開示されたプログラムの問題点」を公開しています。

特に理由がなければ、本稿よりも別稿の方を先にご参照頂いた方がいいと思います。

本節の内容の詳細を（１２）節に書きました。

（１）序論

西浦氏らのグループは、2023-10 に Scientific Reports にコロナワクチンに関する論文 [Kayano 2023] を発表しました。
後に「コロナワクチンで死者9割以上減京都大チームが推計」と共同が報じた論文です。（以下では [Kayano 2023] を Sci Rep 2023 論文、と書きます。）
Evaluating the COVID-19 vaccination program in Japan, 2021 using the counterfactual reproduction number
https://doi.org/10.1038/s41598-023-44942-6

図1.1　Sci Rep 2023 論文の Figure 1（本稿に Figure 1 への言及はありません。）

Sci Rep 2023 論文は、補足情報の Figure S5 に、白丸でデルタ株が検出された症例の割合の実測値を示し、赤線でそれをモデル化しています。論文はこの赤線を、最大値が 1 のロジスティック曲線だと説明しています。

図1.2　Sci Rep 2023 論文、補足情報の Figure S5

しかし Figure S5 の赤線の最大値は 1 ではありません。
本稿は、これを2つの方法で示します。また本稿は、Figure S5 の白丸を改めてモデル化しました。これにより、論文 Figure S5 の赤線よりも白丸に良く適合するモデルが見つかりました。 Figure S5 の赤線は、白丸のモデルとして疑問があります。

本稿に示された計算やグラフは、全てこちらのプログラムで計算しました。

重要な追記を（０）節と（１２）節に書きました。

（２）Figure S5 の赤線は最大値 1 のロジスティック曲線と説明されている

Figure S5 は、Sci Rep 2023 論文の補足情報にある、デルタ株の市中比率を示すグラフ（白丸の実測値と、赤線のモデル値）です。赤線は、最大値 1 のロジスティック曲線だと論文の本文で説明されています。

We assumed that increased with the detected proportion of COVID-19 cases owing to the Delta variant in Japan [60], which was modeled using a logistic curve. We then rescaled up from 1 to a maximum of 1.5 [61–63]. A comparison between the predicted and observed proportion is shown in Supplementary Fig. S5.

が日本においてデルタ株によるCOVID-19症例の検出割合の増加に応じて上昇するものと仮定し [60]、をロジスティック曲線を用いてモデル化した。その後、を1から最大1.5まで再スケーリングした [61–63]。予測された割合と観測された割合の比較は、補足 Figure S5 に示されている。

引用部は、 u_t という文字を再スケーリングの前と後の両方に対して使っているのでやや紛らわしいですが、

(a) 再スケーリング前のを最大値 1 のロジスティック曲線を用いてモデル化し、それを補足 Figure S5 に示した。
(b)（ $論文\ 式(3)$ で用いている）は、(a) を 1～1.5 に再スケーリングしたもの。

と述べています。

したがって引用部は、補足情報 Figure S5 の赤線は「最大値 1 のロジスティック曲線」と説明しています。

（３）Figure S5 の赤線の最大値は 1 ではない

論文は、Figure S5 の赤線を「最大値 1 のロジスティック曲線」と説明しています。ところが実際の赤線の最大値は 1 ではありません。

Figure S5 に、y軸=1.0 の水平線を加筆すると、以下になります。

図3.1　Sci Rep 2023 論文、補足情報の Figure S5 に、y軸=1.0 の水平線を加筆

Figure S5 の赤線は、 y=1.0 に漸近していません。このグラフを右方に幾ら延長しても、1 にはなりません。グラフの右端（x軸 "12"）でのy軸の値を目視で読むと、 0.991 です（目視なので、小数点以下第3位には誤差があると思われます）。

Figure S5 の形状は、（２）節に示した論文の説明と異なります。

（４）Figure S5 の赤線のパラメータの推定

（３）節で述べたことを別の方法で確認するため、本稿は Figure S5 の赤線のパラメータを推定します。

まず最初に、Figure S5 の赤線の x座標 "6", "7", "8", ..., "12" の y座標を、目視で以下のように読み取りました。

x座標	y座標	x座標	y座標
2021-06-18	0.072	2021-10-18	0.989
2021-07-18	0.453	2021-11-18	0.990
2021-08-18	0.897	2021-12-18	0.990
2021-09-18	0.981

表4.1 Figure S5 の赤線の一部の座標（各x座標が「18日」になっている理由の一部は [注4a]）

以下で、表4.1 に適合するロジスティック曲線のパラメータを推定します。

x, y における最大値1のロジスティック曲線は、

$\displaystyle y = \frac{1}{1 + exp(-k \times (x - x0))} 　......\ \ 式(1)$

と表記されます。ここでは、曲線の傾きの鋭さを定めるパラメータであり、は傾き最大の位置のx座標を定めるパラメータです。日付は、2021-06-07 を 1 とする整数（x 値）に変換し、それを式(1) に代入します [注4b]。

との2つのパラメータを定めればこの式は定まるのですが、この式の最大値は 1 です。しかし既に（２）節で Figure 5S の最大値が 1 でないことは分かっているので、パラメータを推定する際に本稿は、以下の式を使います。

$\displaystyle y = \frac{1}{1 + exp(-k \times (x - x0))} \times ry + sy 　......\ \ 式(2)$

式(2) では、式(1) の右辺を倍してを加算しています。本節では、式(1) の $[k,\ x0]$ を推定するのではなく、式(2) の $[k,\ x0,\ ry,\ sy]$ を推定します。推定の結果、y軸方向への伸縮がなければ ry = 1 になります。y軸方向への移動がなければ sy = 0 になります。

$[k,\ x0,\ ry,\ sy]$ の推定は、Nelder-Mead 法の最適化によって行いました。コスト関数としては残差の二乗和を用いました。また最適化の初期値として、暫定的な収束値の周辺でラテンハイパーキューブサンプリングを用いた100個の初期値を用意しました。[注4c]

最適化計算で得たパラメータは以下でした。

k	x0	ry	sy
0.0785	44.118	0.992	-0.002

表4.2 （表4.1のデータに適合する）式(2) のパラメータ

y軸方向への移動のパラメータは 0 に近いので、赤線はy軸方向に移動していないと考えていいと思われます。一方でy軸方向への伸縮のパラメータは 0.992 でした。このパラメータは、赤線が最大値1のロジスティック曲線を縦方向に約0.99倍したものだと示しています。

この計算結果は、（３）節で示した観察（x軸 "12" での赤線の y座標の値が 0.991 ）と整合しています。

[注4a] Figure S5 の右端の白丸の日付が 2021-08-23 であると解すべきである論文の補足情報の記述（"The data were censored on week 34 (from 23 to 29 August 2021)..."）がありました。ここから逆算すると Figure S5 横軸の各月の目盛りは「1日」ではなく「18日」を示しています。
[注4b] 日付から整数への変換に使われている 2021-06-07 は、zenodo での情報開示の File5 の先頭データの日付です。
[注4c] Nelder-Mead 法とラテンハイパーキューブサンプリングのパラメータなど詳細については、計算に用いたプログラムをご参照下さい。

（５）（４）節で推定した曲線と赤線の重ね合わせ（図5.2）

（４）節のパラメータに基づいて描いたロジスティック曲線がこちらです。

図5.1　論文 Figure S5 を本稿が再現したグラフ

このグラフはx軸、y軸の目盛りを含めて Figure S5 の赤線に重なるはずです。図5.1 を緑色の点線にして重ねたところ正確に重なることを確認できました。再現して重ねた緑色の点線は、視覚上区別できない状態で赤線に重なっています。

図5.2　論文 Figure S5（赤線）と、本稿が再現したグラフ（緑点線）の重ね合わせ

（重ね合わせに用いた、背景を透明にしてある再現グラフの画像はこちら。）

（６）Figure S5 の白丸に適合するロジスティック曲線のパラメータの推定

Figure S5 には、赤線の他に測定値と説明されている白丸があります。本節ではこちらのデータを使ったロジスティック曲線のパラメータを求めます。

この白丸の中心のx座標、y座標を目視で以下のように読み取りました [注6a]。

x座標	y座標	x座標	y座標
2021-06-07	0.030	2021-07-19	0.440
2021-06-14	0.050	2021-07-26	0.670
2021-06-21	0.070	2021-08-02	0.790
2021-06-28	0.110	2021-08-09	0.850
2021-07-05	0.210	2021-08-16	0.890
2021-07-12	0.330	2021-08-23	0.920

表6.1 Figure S5 の白丸の中心の座標

（４）節と同様に、これらの点に適合するロジスティック曲線のパラメータを推定します。用いるのは、（４）節と同じ式(2) です。

$\displaystyle y = \frac{1}{1 + exp(-k \times (x - x0))} \times ry + sy 　......\ \ 再掲\ 式(2)$

同様の最適化計算で得たパラメータは以下でした。

k	x0	ry	sy
0.108	43.025	0.912	0.028

表6.2 （表6.1のデータに適合する）式(2) のパラメータ

[注6a] 表6.1 の x座標 2021-07-12 のデータを 0.320 と読み取っていましたが間違いであり、正しい値は 0.330 でした。修正履歴 2025-04-29 に関連を書きました。

（７）（６）節で推定した曲線と白丸の重ね合わせ（図6.1）

（６）節のパラメータに基づいて描いたロジスティック曲線をグラフ化し、それを Figure S5 に重ねました。この緑線は、「赤線ではなく白丸に」適合させています。

図6.1　Figure S5 の白丸に適合するロジスティック曲線を推計したものと、Figure S5 の重ね合わせ

（重ね合わせに用いた、背景を透明にしてあるグラフの画像はこちら。）
本稿が計算した緑線のロジスティック曲線は、論文が「白丸をモデル化した」と説明している赤線よりも、白丸に良く適合しています。このロジスティック曲線を、以下では便宜上「曲線Ａ」と呼ぶことにします。

（８）最小値0・最大値1に固定したロジスティック曲線による白丸への適合

（７）節で計算したのは、表6.1 のデータに適合する式(2) のパラメータのロジスティック曲線でした。本節では、同じデータに適合する式(1) のパラメータを計算してみました。「最小値 0、最大値 1 に限定した白丸に適合するロジスティック曲線はどういうものか」の計算になります。

得られたパラメータは以下でした。

k	x0
0.0895	43.981

表8.1 （表6.1のデータに適合する）式(1) のパラメータ

このパラメータによるグラフを Figure S5 に重ねると、こちらになります。

図8.1　Figure S5 の白丸に適合する、条件の厳しいロジスティック曲線を推計したものと、Figure S5 の重ね合わせ

（重ね合わせに用いた、背景を透明にしてあるグラフの画像はこちら。）
図8.1 は、4パラメータの図6.1 より少ない2つのパラメータで白丸に適合させています。白丸への適合は、図6.1 の方が良いです。その代わり図8.1 は、正確に最小が 0 で最大が 1 のロジスティック曲線になっています。

（９）結果

Sci Rep 2023 論文の Figure S5 の赤線は、論文では「最大値1のロジスティック曲線」と説明されています。しかしグラフの赤線が漸近しているのは y=1 ではなく、約0.99 でした。

Figure S5 の赤線の一部の座標を目視で読み取り、これらに適合するロジスティック曲線のパラメータを最適化計算で推計し、S5 の赤線を再現しました。再現したグラフを S5 に重ね合わせたところ、正確に重なりました。得られたパラメータによると、赤線の最大値は約0.99 です。

同様にして、Figure S5 の白丸に適合するロジスティック曲線のパラメータを最適化計算で推計しました。得られたパラメータのロジスティック曲線を Figure S5 に重ねると、白丸に良く適合しました。

（１０）考察

Figure S5 赤線の再現を意図して（４）節で推定したパラメータで描いたグラフは、S5 赤線と正確に重なりました。このことは、表4.1 に示した目視によるデータや、本稿のパラメータ推計の妥当性を強く裏付けています。

Figure S5 の赤線は「測定値である白丸に適合するロジスティック曲線のモデル」として示されています。赤線の最大値は約0.99 だと思われます。論文は、赤線が最大値1のロジスティック曲線だと説明しているのに、なぜ最大値が異なる曲線をモデルとして示したのでしょうか。

「最大値が1のロジスティック曲線をモデルにしようとしたのだが、白丸に適合するロジスティック曲線を探したところ、最大値が約0.99 の S5 の赤線が良く適合したので、赤線を採用した」という事情でしょうか。論文のようなモデルを作成する場合、測定値に適合させるために理想的な性質（最大値1）とは異なる性質（最大値約0.99 ）のモデルが用いられることは、一般論としてあり得ます。

しかし Figure S5 の場合は、こうした事情だとは考えられません。そもそも Figure S5 を見ると、赤線を修正すれば、白丸と赤線をさらに適合させる余地があることは容易に見て取れます。赤線よりも傾きの大きな曲線ならば、6月上旬の白丸への適合と、7月下旬の白丸への適合を同時に向上させることができそうだからです。実際（６）節、（７）節に示したように、白丸に良く適合したのは、赤線（ k=約0.0785 ）よりも大きな傾きの曲線Ａ（ k=約0.108 ）でした。論文が、白丸に良く適合するロジスティック曲線を探したのなら、曲線Ａ（あるいはそれに近い曲線）を採用すべきでした。

論文が計算の詳細を示していないので、赤線ではなく曲線Ａを白丸のモデルにした場合の計算結果への影響ははっきりしません。しかし、パラメータが赤線と曲線Ａで違うため、曲線が増加するのに要する日数は両者で大きく異なります。

曲線	式(2)のパラメータ	y軸が0.1から0.9 になるまでの日数	y軸が0.1から0.95 になるまでの日数
Figure S5 の赤線に適合させた曲線	0.0785	56.0	65.5
Figure S5 の白丸に適合させた曲線Ａ	0.108	40.7	47.6

表10.1 赤線と曲線Ａにおける0.1から0.9や0.95になるまでのおよその日数

y軸が 0.1 から 0.9 に変化する日数は、赤線だと約 56 日なのに対し、曲線Ａでは約 41 日ですから大きく異なります。この事情は、 $論文\ 式(3)$ にあるスケーリング・パラメータの値によらず維持されるため、計算結果に小さくない影響を与えると考えられます。

論文は、白丸のモデルとしてさらに適合するロジスティック曲線の存在が容易に推察できる状況なのに赤線を採用した理由や、曲線Ａ（に近い曲線）をモデルとして採用しなかった理由を説明する必要があります。

（１１）結論

以上の検討から、Sci Rep 2023 論文における Figure S5 の赤線には、論文が主張するロジスティック曲線モデルとしての意図や整合性に疑義があります。赤線は、デルタ株比率の実測値である白丸のモデルとしての妥当性に疑問が生じています。赤線は、 $論文\ 式(3)$ の u_t を通じて d_t や $R_{ab,t}$ に連鎖的影響を与えます。この論文は、Figure 1 を示しながら、論文のモデルが観測データをうまく捉えられた（"our transmission model successfully captured the observed data ..."）と述べていますが、基礎のデルタ株比率のモデル化に疑問があります。本稿が示しているのは単なる図の不整合ではなく、反実仮想シナリオを使った計算の正当性に関わる疑問です。デルタ株比率モデルの検証のためにも、論文の計算データや計算コードの開示が不可欠です。[注11a]

[注11a] 2025-04-19 に、論文の計算データや計算コードが zenodo https://zenodo.org/records/15244462 で開示されました（ただし、HER-SYS データを除く）。開示データされたデータには幾つかの問題があります。それらについては別途検討する予定です。

（１２）本稿公開後に示された、論文の開示情報について（その２）

本節では（０）節の内容を詳しく述べます。

本稿は（４）節に書いたように、コスト関数として残差の二乗和を用いて検討しました。一方で西浦氏が論文で使ったコスト関数は別の形であったことが、2025-04-19 の zenodo での情報開示で分かりました。
私は、この開示情報に

(a) 開示情報が論文のグラフ Figure S5 を再現しない。
(b) コスト関数が（実質的に無数の局所極小があるので）不適切。
(c) 初期値設定が（単一初期値なので）不適切。

などの問題があることを別稿で指摘しています。

(a)～(c) のうち特に (b)「（開示情報の）コスト関数が不適切」があるので、本稿はこのままとします。

情報開示によれば、本稿のコスト関数は論文のコスト関数とは異なるのですが、論文のコスト関数に存在する重大な問題が本稿のコスト関数には存在しないからです。これは、私がそうした問題が発生しないようにコスト関数を作成したからです。（ただし、本稿のコスト関数が特別なものだから問題が発生していないのではありません。論文のコスト関数が特別に問題なのであり、本稿のコスト関数はいわば普通のものです。）同じことですが、本稿のコスト関数は、（不適切な性質のある）論文のコスト関数の対案の一例になっています。ただし、本稿のコスト関数である残差の二乗和にも「外れ値があると、これに関するコストの割合が大きくなるため、結果が外れ値に引きずられる」との問題があります。別稿の（付録Ｅ）の末尾には、コスト関数の他の対案を示しています。

更新履歴

2025-03-31
公開。
2025-04-01
グラフの体裁を修正しました（点線にしていたものの一部を実線に。紛らわしいグラフタイトルを削除）。論旨に変更はありません。
2025-04-03
以下を修正しました。これらによる論旨の変更はありません。
- （４）節に「コスト関数としては二乗和を用いました。」との説明を追加しました。
- 表10.1 の2つの数字の誤記を訂正しました。65.4 は 65.5 が正しく、40.0 は 39.9 が正しい値でした。
2025-04-23
2025-04-23 時点のこのページのアーカイブを取得しました。こちらです。
2025-04-24
以下を修正しました。これらによる論旨の変更はありません。（以下の修正は比較的大きいので、修正前の状態を修正履歴 2025-04-23 に示したアーカイブに置いてあります。）
- 「表3.1」「表3.2」はそれぞれ「表4.1」「表4.2」とすべきだったので修正しました。
- 表4.1 と表6.1 に「x座標の日付を17日後にシフトする修正」を行いました。西浦氏が zenodo で行った情報開示の File5 と、表6.1 とを照合した際に修正の必要に気付いたのですが、そもそも [注4a] の事情があったのでこの問題には情報開示前から気づくべきでした。失礼しました。関連して、計算プログラムの日付データを 17日分シフトしたので、日付に関する計算結果が 17 増え、グラフの横軸も修正されました。変化した計算結果は表4.2 の x0、表6.2 の x0、表8.1 の x0 です。一連の修正は座標データの横方向へのシフトに関する事項なので、（５）節、（７）節での重ね合わせの議論や傾きに関する議論の論旨には影響しません。例えば、表10.1 は修正する必要がありません。
- 表10.1 で「0.0785」とすべきところを「0.785」としていたので修正しました。
2025-04-28
以下を修正しました。これによる論旨の変更はありません。
- 日付を整数値に変換する際、本稿では「2021-05-20 を 0」が基準でしたが、zenodo で開示されたプログラムは、「2021-06-07 を 1」が基準です。2つの基準があると検討しにくいので、本稿の基準を「2021-06-07 を 1」に変更しました。この結果、日付に関する計算結果が 17 減りました。（2025-04-24 の修正と変更の幅が同じですが、偶然です。）影響を受けるのは、表4.2 の x0、表6.2 の x0、表8.1 の x0 です。[注4b] に関連事項があります。
2025-04-29
データの読み取りに誤りがあったので修正しました。失礼しました。これにより計算結果や図が変化しましたが、論旨の変更はありません。修正した複数の表や図についての詳細は、こちらをご参照下さい。
2025-06-13
（１２）節を追加しました。また（１）節の末尾に「（１２）節を追加した」の旨を書きました。
2025-08-24
- （０）節を追加しました。（１２）節を改稿しました。
- コスト関数を単に「二乗和」と表記していましたが、これを「残差の二乗和」に変更しました。これによる論旨の変更はありません。

2025-02-19

西浦氏の Scientific Reports 論文について（９）論文 Figure 1 の fit は当然なのでは

「接触8割減」の問題を 2024年時点でまとめた論考はこちらに。
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

西浦氏が2025-08 に示した「接触8割減」の数理モデルについての問題はこちらに。
https://x.com/sarkov28/status/1988558334849609903
https://x.com/sarkov28/status/1989284028713963820

私がネット上でしていることのまとめは、こちらに。
https://sarkov28.hatenablog.com/entry/2022/03/29/160915

2025-12-25 の追記：後日の検討により、本稿の主たる内容には修正すべき点があると考えています。しかし本稿が検討している西浦氏の論文には、他にも様々な問題があります。別稿（７）や別稿（１）では「論文が計算している数値を現実の感染者数や死者数と比較すべきではない」という問題を説明しています。

2025-12-25 の追記：後日の検討により、本稿の主たる内容には修正すべき点があると考えています。しかし本稿が検討している西浦氏の論文には、他にも様々な問題があります。別稿（７）や別稿（１）では「論文が計算している数値を現実の感染者数や死者数と比較すべきではない」という問題を説明しています。

（１）序論

西浦氏らのグループは、2023-10 に Scientific Reports にコロナワクチンに関する論文 [Kayano 2023a] を発表しました。
後に「コロナワクチンで死者9割以上減京都大チームが推計」と共同が報じた論文です。（以下では [Kayano 2023a] を Sci Rep 2023 論文、と書きます。）
Evaluating the COVID-19 vaccination program in Japan, 2021 using the counterfactual reproduction number
https://doi.org/10.1038/s41598-023-44942-6

図1.1　Sci Rep 2023 論文の Figure 1

Sci Rep 2023 論文の Figure 1 では、（数理モデルを使わずに）観測値から計算されたオレンジの dot と、（数理モデルを使って計算された）緑の line とが、かなり近い値を示しています。この状況は「よく fit している」などと表現されることがあります。本稿はこの表現についての疑問を検討します。このグラフの計算方法は必ずしも明らかではなく、計算方法によっては、「Figure 1 の fit は当然」だからです。

この論文は、計算手順の記述が分かりにくく、実効再生産数 $R_{ab,t}$ の計算手順が明確ではありません。本来なら明確であるべきこうした事項がはっきりしないのは、Sci Rep 2023 論文が、計算に用いたソースコードを開示していないからでもあります。ソースコードは開示されるべきであり、開示されていれば本稿の議論は不要です。この論文の問題点を論じている [Kakeya 2024]、[Kakeya 2025]、[Nakamura 2024a]、[Nakamura 2024b] も、論文が用いたソースコードを開示する必要があると指摘しています。

本稿は、年齢層別の実効再生産数 $R_{ab,t}$ を計算した可能性のある2つの数式を検討し、これを通じて Figure 1 の fit は当然なのでは、との問いを考察します。

（２）節では、Sci Rep 2023 論文における新規感染者数の計算方法を示します。（３）節では、年齢層別の実効再生産数の計算方法について考察します。（４）節では、（３）節を踏まえた検討を行います。（５）節では、「論文 Figure 1 の fit は当然なのでは」との問いを検討します。（６）節では、本稿での考察が反実仮想シナリオ計算に与える影響を検討します。（７）節では、本稿の結論を述べます。

図1.2 は、本稿の検討の概要を示したものです。

図1.2　本稿の検討の概要

Sci Rep 2023 論文については、複数の記事で書いています。

なお、「Figure 1 の fit は当然」である場合、私の一連のブログ記事の幾つかには修正が必要になります。記事（４）は一部ですが、記事（５）と記事（６）は全面的な書き換えが必要です。この点については各記事に説明を追加します。ただし、これ以外の記事への影響はありません。例えば（７）「ワクチンで感染者が９割減」は誤りには影響ありません。

（２）論文式(2) や式(3) における新規感染者数の計算

論文によると、式(2) や式(3) で用いる新規感染者数の計算手順は以下です。

論文には、発症から報告までの遅れを表す確率密度関数と、感染から発症までの遅れを表す確率密度関数が示されています。論文の付録には全年齢層の報告日基準の感染者数しかありませんが、論文著者の手元には、年齢層別の発症日基準の感染者数と報告日別の感染者数があります。

これらデータのうち、報告日しか分からないものに対して、発症から報告までの確率密度関数の畳み込み積分の逆計算を行い、発症日基準の新規感染者数を得ています。さらに発症日基準の新規感染者数に対し、感染から発症までの確率密度関数の畳み込み積分の逆計算を行い、感染日基準の新規感染者数 $i_{a,t}$ を得ています。

（３）考察：年齢層別の実効再生産数の計算方法

(3-1) 年齢層別の実効再生産数に関係する式(2) と式(3)

既に（２）節の方法で、年齢層別、感染日基準の新規感染者数 $i_{a,t}$ が計算できています。論文には、実効再生産数を計算する可能性のある式が2つあります。

$\displaystyle i_{a,t} = \sum_{b=1}^{10}\ \sum_{τ=1}^{t-1}\ R_{ab,t}\ i_{b,t-τ}\ g_{τ} ......\ \ 論文\ 式(2)$

$\displaystyle R_{ab,t} = \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right) K_{ab}\ p\ h_t\ d_t\ c_t\ \ ......\ \ 論文\ 式(3)$

ここで、 $i_{a,t}$ は感染日基準の新規感染者数、, は年齢層、は時刻です。

$論文\ 式(2)$ は、再生方程式 renewal equation であり、時刻 t の新規感染者数を、過去の新規感染者数から計算しています [注3-1a]。一方で $論文\ 式(3)$ は、実効再生産数 $R_{ab,t}$ を "decomposed" 「分解した」ものだと論文で説明されています。

以下では、 $論文\ 式(2)$ で $R_{ab,t}$ を計算したとの考え方を「式(2)説」、 $論文\ 式(3)$ で計算したとの考え方を「式(3)説」と呼びます。これらは一般的な呼称ではなく、本稿が便宜的に導入したものです。

[注3-1a] renewal equation の訳語としては、他に更新方程式、再生産方程式があります。再生方程式は例えば [稲葉 2020] 第2章。

(3-2) 式(3)説の検討

(3-2-1) 式(3)説の詳細

「実効再生産数 $R_{ab,t}$ を計算したのは、 $論文\ 式(3)$ である」との式(3)説について説明します。

式(3)説の場合、 $R_{ab,t}$ の計算詳細は以下になります。

(3-2-1a) （２）節の方法で、年齢層別、感染日基準の新規感染者数 $i_{a,t}$ が計算できています。
(3-2-1b) $論文\ 式(8)$ を用いて最尤推定を行い、パラメータを得ます。
(3-2-1c) $論文\ 式(3)$ の右辺における各項の（各 t での）値は分かっているので、これらを用いて、 $R_{ab,t}$ を計算します。

(3-2-2) 式(3)説の成立に肯定的な事項

(3-2-2-1) 式(3)説の成立を前提とした言説

Sci Rep 2023 論文の Figure 1 の計算方法に言及している言説の多くは、式(3)説を採っています。私も式(3)説を採った記事を書いています。

[Kakeya 2024], [Kakeya 2025] は、式(3)説を採っています。
私のブログ記事（５）と記事（６）は、式(3)説を前提にしています [注3-2-2-1a]。
枇杷氏による Sci Rep 2023 論文についてのスレッドは、「実測された感染状況とよく一致した」などと説明しているので、式(3)説を採っていると思われます。

[注3-2-2-1a] ブログ記事（４）の一部にも式(3)説を前提とした記述があります。

(3-2-2-2) 論文の記述

Sci Rep 2023 論文には以下の記述があります。

we tried to indirectly capture its impact via estimating the effective reproduction number using several explanatory variables, including mobility.

我々は、移動性を含むいくつかの説明変数を用いて実効再生産数を推定することで、その影響を間接的に捉えようと試みた。

この引用部にある「移動性を含むいくつかの説明変数を用いて（略）推定する」は $論文\ 式(3)$ を指していると考える他ないので、ここは式(3)説を述べているようにも読めます。ただしこの引用部は、 $R_{ab,t}$ の計算について述べたのではなく、単に式(3) を描写しただけの可能性もあり、その場合はどちらの説も述べたことにはなりません。

なお論文には、

We developed the time-dependent transmission model that accounts for heterogeneous transmission between age groups, fitting the model to observed incidence data and estimating unknown parameters.

我々は、年齢層間の異質な伝播を考慮した時間依存の感染伝播モデルを開発し、観測された感染データにモデルを適合させ、未知のパラメータを推定した。

との記述もあります。このうち "estimating unknown parameters"「未知のパラメータを推定した」は式(3) での処理を指していると思われますが、"fitting the model to observed incidence data"「観察された感染データにモデルを適合させ」が式(3) 、式(2) のどちらでの処理なのかは不明であり、したがってこの引用部が式(2)説、式(3)説のどちらを述べているのかは、はっきりしません。

(3-2-3) 式(3)説の成立に否定的な事項

式(3)説を採る場合、数理モデルによる全年齢層の新規感染者数は、以下の方法で計算されているか、少なくとも以下の方法で計算された値と大きく乖離しないはずです [注3-2-3a]。

$論文\ 式(3)$ で $R_{ab,t}$ を計算し、 $R_{ab,t}$ を用いて年齢層別の新規感染者数を計算し、それを全年齢層で合計して全年齢層の新規感染者数を得る。

計算した全年齢層の新規感染者数は、Figure 1 に緑の line で示されています。 Figure 1 の緑の line と、（（２）節の方法で）報告値から計算されたオレンジの dot とに、視覚上に大きな乖離はありません。

したがって式(3)説を採る場合、 $論文\ 式(3)$ の右辺は、以下の両方の性質を備えていることになります [注3-2-3b]。

(3-2-3a) $論文\ 式(3)$ の右辺が適切であり、左辺の実効再生産数 $R_{ab,t}$ の性質をかなり適切に捉えている。論文の "decomposed"「分解」は適切である。
(3-2-3b) $論文\ 式(3)$ の右辺の各項が、適切な値を示している。

Figure 1 を「よく fit している」と表現するのは、（容易に成立するとは思えない）この2つが成立しているとの考えからです。

$論文\ 式(3)$ の右辺の先頭部分に、

$\displaystyle \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right)$

という項があります。各項目は、以下を表しています。

は、全人口の比率。
$l_{a,t}$ は、 $論文\ 式(1)$ で計算されるワクチンによる免疫保持者の比率。
（"the immune fraction in age group a at calendar time t"）
$\displaystyle \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a}$ は、感染による免疫保持者の比率。
（"the immune fraction owing to [...] infections"）

したがってこの右辺の先頭部分は、感受性者比率を表しています。(3-2-3-1)節～(3-2-3-3)節では、ここにある問題を指摘し、 $R_{ab,t}$ が不適切な値になっていることを示します。この場合、式(3)説で考えると Figure 1 に小さくない乖離があるはずですが、実際にはある程度 fit しています。よってこれらは式(3)説に否定的な事項です。

[注3-2-3a] ここに大きな乖離がある場合、論文の計算の中にあってはならない不一致があることになります。
[注3-2-3b] (3-2-3a) と (3-2-3b) とが適切でなくても、Figure 1 のオレンジの dot と緑の line が大きく乖離しない可能性はゼロではありません。ある原因で両者が乖離しそうになっても、別の原因がそれを相殺すれば、結果的に両者が乖離しない可能性はあります。しかしこれは一般には生じない極めて稀な状況なので、これが論文 Figure 1 に関する計算で起きたと考えるのは、妥当ではありません。

(3-2-3-1) ワクチンによる免疫の項の問題

$論文\ 式(3)$ の右辺には、ワクチンによる免疫保持者の比率の項 $l_{a,t}$ が組み込まれています。「ワクチンが有効ならば感染しない」のですから、ここで使われているワクチンの効果は感染予防効果でなければいけません。

しかし別記事（８）論文のワクチン感染予防効果への疑問で示したように、この論文がワクチンの効果の参照先として挙げている [Goldberg 2021] と [Tartof 2021] が計算しているのは、感染予防効果ではなく発症予防効果に近いものであり [注3-2-3-1a]、 $論文\ 式(3)$ 右辺のうち $l_{a,t}$ は、不適切に大きな値になっています [注3-2-3-1b]。

したがって式(3)説で考えると、実効再生産数 $R_{ab,t}$ は、適切な値よりも小さくなっています。（ただし、どれだけ大きな値になっているかは不明です。）

[注3-2-3-1a] [Goldberg 2021] と [Tartof 2021] は、「医療データベースに登録された感染者」を計算対象としている。このデータは、Sci Rep 2023 論文の $論文\ 式(3)$ の意味における感染者ではない。少なくとも $論文\ 式(3)$ の意味における感染者のうち「無症状で診断を受けずに検査陽性にならなかった人」はデータに含まれていない。両論文は、計算に用いたデータにある幾つかのバイアスの解消を試みているが、本稿が問題視しているバイアスの解消は試みられていない。この点については、別記事で考察した。
[注3-2-3-1b] ワクチンの感染予防効果と（感染以降の発症などの状況を防止する効果が混在した）その他の効果の vaccine effectiveness の大小関係は不明である。しかし、 $論文\ 式(1)$ が使用しているパラメータ h_s は「その効果で守られている人の人口中の割合」なので、常に (感染予防効果) < (（感染以降の発症などの状況を防止する効果が混在した）その他の効果) となる。

(3-2-3-2) 感染による免疫の項の問題

$論文\ 式(3)$ 右辺には、感染による免疫保持者の比率の項

$\displaystyle \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a}$

が組み込まれています。これは、Sci Rep 2023 論文の計算開始日である 2021-02-17 から t - 1 までの年齢層の新規感染者数 $i_{a,t}$ を累計し、人口に対する比率を計算したものです。

ワクチン接種による免疫計算の開始日を 2021-02-17 にすることには、合理的根拠があります。この日が日本におけるワクチン接種の開始日だからです [注3-2-3-2a]。

しかし感染による免疫の計算開始日を 2021-02-17 にする合理的根拠があるとは思えません。論文にもその理由の記載はありません。この計算開始日は、「ワクチン接種の開始日と同じ日」との便宜的理由で決められたと思われます。

$論文\ 式(3)$ は、

2021-02-17 以降に感染した人は 2021-11-30 まで減衰しない感染予防免疫を得た。
2021-02-16 以前に感染した人は全く感染予防免疫を得なかった。

としています。現実の免疫の効果がこのように不連続に変化するはずはないので、論文の考え方は非合理的です。

この非合理的な考え方のため、本節冒頭に示した感染による免疫保持者の比率の項は、不適切に小さな値になっています。式(3)説ならば、 $R_{ab,t}$ はこの影響で適切な値よりも大きくなっています。

本節で述べている効果が無視できない大きさであることを概算できます。一例として、感染による免疫の計算開始日を 2021-02-17 から 2021-01-01 に変更し、この変更が新規感染者数に与える影響を、論文 Figure 1 のピーク付近の 2021-08-15 で考えます。計算開始日変更によって新規感染者数の累計は 182938 人増えるので、 $論文\ 式(3)$ で考えると日々の実効再生産数 $R_{ab,t}$ は約 1-(182938/N) 倍になります。（N は全人口。式(3) は年齢層別なのでこれは概算。）この場合、日々の新規感染者数は $論文\ 式(2)$ から 1-(182938/N) 倍されるため、2021-08-15 における影響は (1-(182938/N))¹⁸⁰ 倍であり、これは約0.8倍になります [注3-2-3-2b]。つまり式(3)説で本節が指摘する効果を考慮すると、適切な Figure 1 の緑の line は、2021-08-15 に約2割下方に移動し、fit しなくなります。

それほど多数ではない新規感染者数の増加が、「波」のピークを約2割下げるとの大きな変化をもたらすのは、ここに関与するのが（Sci Rep 2023 論文が述べている、実効再生産数を経由した）間接的効果だからです。

[注3-2-3-2a] NHK 2021-02-17「新型コロナワクチン先行接種始まる医療従事者約4万人対象」 [アーカイブ]。
[注3-2-3-2b] 182938 人は、2021-01-01～2021-02-16 の新規感染者数。180 日は、2021-02-17 から 2021-08-15 までの日数。全人口 N は、126146000。「182938/N の影響が、180日累積する」との考え方で計算している。新規感染者数は、厚生労働省「データからわかる－新型コロナウイルス感染症情報－」https://covid19.mhlw.go.jp/extensions/public/index.html 「新規陽性者数の推移（日別）」の、"ALL" から。全人口は「人口推計」https://www.stat.go.jp/data/jinsui/2023np/index.html の 2020-10-01 時点の人口から。

(3-2-3-3) ワクチンによる免疫の項と、感染による免疫の項の問題

(3-2-3)節冒頭に示した

$\displaystyle \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right)$

は、感受性者比率を表しています。論文が限界（limitations）として指摘しているように、ここには問題があります。

この感受性者比率の計算方法は、ワクチンによる免疫保持者と感染による免疫保持者とに、重なりがないこと（両者が排反であること）を前提にしています。この式が妥当であるためには、

(3-2-3-3a) ワクチン接種によって $l_{a,t}$ の意味で免疫を得ている人は、感染しない。
(3-2-3-3b) 研究期間中に感染した人は、ワクチンを接種しない。

の両方が成立する必要があります。このうち、(3-2-3-3a) は（パラメータ $l_{a,t}$ の定義から）成立していると思われます。しかし、(3-2-3-3b) が厳密に成立していないことは明らかです。研究期間中の感染者の中には、ワクチンを接種した人が一定数存在したはずだからです [注3-2-3-3a]。これらの人の比率の分、本節冒頭に示した項は不適切に小さくなっています。式(3)説ならば、 $R_{ab,t}$ はこの影響で適切な値よりも小さくなっています。（ただし、どれだけ大きな値になっているかは不明です。）

[注3-2-3-3a] 専門家も既感染者の接種を妨げていません。厚生科学審議会予防接種・ワクチン分科会は資料１の「既感染者への接種について」との資料で、「新型コロナワクチンについては、現在の予防接種実施規則、臨時の予防接種実施要領においては、既感染者を対象から除外せず、事前の感染検査を不要としている。」と示しています。（2021-05-21 厚生科学審議会予防接種・ワクチン分科会資料１ https://www.mhlw.go.jp/content/10601000/000783070.pdf）

(3-3) 式(2)説について

(3-3-1) 式(2)説の詳細

「実効再生産数 $R_{ab,t}$ を計算したのは、 $論文\ 式(2)$ である」との式(2)説について説明します。

式(2)説の場合、 $R_{ab,t}$ の計算詳細は以下になります。

(3-3-1a) （２）節の方法で、年齢層別、感染日基準の新規感染者数 $i_{a,t}$ が計算できています。
(3-3-1b) $論文\ 式(2)$ の $i_{a,t}$ とが分かっているので、これらを用いて、 $R_{ab,t}$ を計算します。

(3-3-2) 式(2)説の成立に肯定的な事項

(3-3-2-1) 論文の記述

Sci Rep 2023 論文には以下の記述があります。

A transmission model was fitted to the confirmed cases from 17 February to 30 November 2021.

感染伝播モデルを、2021-02-17 から 2021-11-30 までの確定症例に適合させた。

この transmission model が、 $論文\ 式(2)$ だけを指しているのか、式(3) を含むのかは判然としません。しかし、この "was fitted" が式(3) での（最尤推定を経由した）計算を含んだものであるなら、この記述は簡潔すぎます。この点を重視するなら、この記述は式(2)説を示していることになります。

(3-3-2-2) 西浦氏の投稿

Sci Rep 2023 論文公開から約一年後の 2024-09-09、西浦氏は、x.com に以下を投稿しました。 https://x.com/nishiurah/status/1833003273248510343

元々の実効再生産数をR(t)=(1-p(t))f(t)として（ここでp(t)は予防接種で防がれた比率、f(t)はそれ以外の時刻成分）R(t）とp(t)は既知ですからf(t)を毎日計算し、反事実R'(t)=f(t)にすれば再現可能ですねー。オープンデータだけでもやってみましたが。

そもそもこの投稿は、Sci Rep 2023 論文とは関係ない話をしている可能性もあります。またここにおける「オープンデータ」が何を指しているのかは、はっきりしません。しかし投稿中の「R(t)=(1-p(t))f(t)」という式は、 $論文\ 式(3)$

$\displaystyle R_{ab,t} = \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right) K_{ab}\ p\ h_t\ d_t\ c_t$

から年齢層 a, b に関する記述を除いたものと式の構造が一致しています。

もしこの投稿が、Sci Rep 2023 論文の計算についてのものなら、これは式(2)説を述べています。なぜならこの投稿は、「式(3) に相当する式を使う時に実効再生産数 R(t) は既知」だとしていますが、この実効再生産数は、式(2) を使って計算する以外に方法はありません。

(3-3-2-3) 同時期に発表された論文が式(2)説に該当する方法で計算

西浦氏は、Sci Rep 2023 論文の発表に前後して、[Kayano 2023b] を発表しています。

[Kayano 2023b] も、反実仮想シナリオ counterfactual scenario を使った論文なので、計算手法として Sci Rep 2023 論文との共通点があります。もちろんこの2つの論文には違いもあります。研究対象にする期間、対象の地域、数理モデルの一部などです。

[Kayano 2023b] も Sci Rep 2023 論文と同様に、研究期間における実効再生産数を計算し、それを一定の方法で変更することにより反実仮想シナリオを作成しています。ここでの計算手順の記述は疑問の余地がないほど明確とは言えませんが、Sci Rep 2023 論文よりは分かりやすいです。[Kayano 2023b] は、本稿における式(2)説に該当する方法で実効再生産数を計算していると思われます。

同時期に手法が類似した論文を2つ発表したとしても、そこにおける主たる計算手順が同じである必要はありません。しかしもし異なる手順を使ったのならそれを説明はすべきでしょう。どちらの論文の読者に対しても紛らわしいからです。2つの論文にそうした記述はありません。

(3-3-3) 式(2)説の成立に否定的な事項

(3-3-3-1) 論文の Figure 1

Sci Rep 2023 論文の著者が、最初のグラフとして Figure 1 を示している理由を検討します。

式(2)説を前提とすると、Figure 1 のオレンジの dot と緑の line がかなり fit するのは計算上の仕様であり、当然です。測定値である dot から実効再生産数を計算し、その逆計算をすれば line の値が得られるからです（この点については、後の（５）節で改めて説明します）。つまりこの場合、Figure 1 の fit の状況をあえて最初のグラフとして掲げる意味は、極めて乏しいです。

Figure 1 には、dot や line の他に、緑の line の周囲にわずかに見える、95%信頼区間があります。しかしこの信頼区間は論文で詳しく論じられていません。またこの信頼区間の計算方法には疑義があり、[Kakeya 2024]、[Kakeya 2025] でも問題視されています。よって信頼区間を示すために Figure 1 を掲げたと考えるのはあまり合理的ではありません。

したがって式(2)説の場合、Figure 1 が最初に掲げられていること自体がやや不合理となります。まるで Figure 1 の fit に意味があるかのような誤解を招くからでもあります。

結局、式(2)説ならば最初のグラフとして掲げられていることがやや不合理となる Figure 1 が、実際には最初に示されているのですから、この事情は式(2)説の成立に否定的な事項となります。ただし、これはいわゆる状況証拠です。

（４）考察：式(2)説と式(3)説どちらが有力なのか

式(2)説と式(3)説に関して、それぞれ肯定的な事項と否定的な事項を検討してきました。どちらかの説は成立するので、片方の成立に肯定的な（否定的な）事項は、他方の成立に否定的な（肯定的な）事項です。

(3-2-2)節で検討した各事項は式(3)説を強く支えることはありません。一方、(3-2-3)節で検討した各事項には一定の合理性があり、特に (3-2-3-2)節で示した概算は、例示ではありますが比較的強く式(2)説を支えます。(3-3-2)節で検討した各事項はさほど強くはありませんが、式(2)説を支えます。(3-3-3)節の事項は式(2)説に否定的ですが、その主張は弱いです。

これらを総合して現時点では、式(2)説が成立する可能性が高いと考えられます。ただしこの場合、「なぜ Figure 1 が最初のグラフとして示されているのか」との (3-3-3-1)節で述べた疑問が残ります。

（５）考察：式(2)説ならば Figure 1 の fit は当然

（４）節の検討を踏まえ、式(2)説（式(2) を用いて、実効再生産数 $R_{ab,t}$ を計算したとする説）での Figure 1 の fit について考えます。

$論文\ 式(2)$ を再掲します。

$\displaystyle i_{a,t} = \sum_{b=1}^{10}\ \sum_{τ=1}^{t-1}\ R_{ab,t}\ i_{b,t-τ}\ g_{τ} ......\ \ 論文\ 式(2)$

式(2)説の場合、Figure 1 の緑の line は以下の手順で計算されます。

(5a) 既に（２）節の方法で、Figure 1 のオレンジの dot を描くための新規感染者数 $i_{a,t}$ が計算できています。
(5b) $論文\ 式(2)$ の $i_{a,t}$ とが分かっているので、これらを用いて、 $R_{ab,t}$ を計算します。
(5c) 再び $論文\ 式(2)$ を用いて、(5b) で得られた実効再生産数から、感染日基準の新規感染者数を計算し、これを全年齢層で合計して全年齢層の新規感染者数を得ます。
(5d) 得られた全年齢層の新規感染者数を Figure 1 の緑の line とします。

ここで (5c) は、(5b) の逆の計算をしているだけです。よって得られた (5d) の全年齢層の新規感染者数は、(5b) の新規感染者数 $i_{a,t}$ の合計値をほぼ完全に再現するはずです。したがって、(5b) のグラフである（Figure 1 の）オレンジの dot と、(5d) のグラフである緑の line は、計算の仕様としてほとんど一致するはずであり、fit するのは当然となります。

この場合、Figure 1 を「よく fit している」などと表現するのは不適切になります。（当然のことだからです。）同様に、「Figure 1 が fit しているからこの論文の数理モデルは適切なのだ」などと考えることも不適切です。fit するのは当然だからです。論文の数理モデルが適切かどうかは、Figure 1 の fit とは別の問題であり、次の（６）節でこれを検討します。

（６）考察：式(2)説の場合の反実仮想シナリオ計算への影響

そもそも Sci Rep 2023 論文は、

(6a)（かを用いて）年齢層別の実効再生産数 $R_{ab,t}$ を計算し、
(6b) （ワクチンなしなどの条件下での）を用いて、(6a) の $R_{ab,t}$ から反実仮想シナリオでの $R_{ab,t}$ を計算し、
(6c) その $R_{ab,t}$ における新規感染者数 $i_{a,t}$ を計算する、

との手順で反実仮想シナリオ counterfactual scenario における新規感染者数 $i_{a,t}$ を得ています。

（式(2)説、式(3)説のどちらだとしても）式(3) の各項には、(3-2-3-1)節、(3-2-3-2)節、(3-2-3-3)節で挙げた問題があります。この3つの節の問題は、以下のように Sci Rep 2023 論文の計算に影響します。

(6d) 式(3)説の場合には (6a) の計算に影響を与えます（＝(3-2-3)節で検討した事項）。これは Figure 1 が fit しなくなるとの効果をもたらします。
(6e) 式(2)説の場合には (6b) の計算に影響を与え、(6b) で計算される $R_{ab,t}$ の値を不適切にし、さらに (6c) で計算される新規感染者数 $i_{a,t}$ を不適切な値にします。

（４）節で検討したように、本稿は式(2)説の可能性が高いと考えています。したがって (6e) に述べた意味で、論文の反実仮想シナリオにおける新規感染者数は、不適切な値になっている可能性が高くなります。

この論文では最初のグラフとして Figure 1 が示されていますが、式(2)説の場合のグラフの dot と line が fit するのは計算の仕様上当然であるのに、読者はあたかもそれが論文の数理モデルの適切さを示したものであるかのように受け取ってしまうかも知れません。式(2)説ならばそれは間違いになります。またこの場合のモデルには、反実仮想シナリオでの実効再生産数 $R_{ab,t}$ や新規感染者数 $i_{a,t}$ に (6e) の不適切さがあり、しかもこれらの検証は困難です。このような論文の構造により、読者が論文の計算結果を適切なものだと誤解する可能性があります。実効再生産数や新規感染者数の適切さについては、(3-2-3-1)節、(3-2-3-2)節、(3-2-3-3)節で述べた問題の定量による検証や、感度分析などによる検証を検討すべきです。

なお、本節を含む本稿全体で用いている実効再生産数（あるいは新規感染者数）の「適切さ」とは、「論文著者が意図した反実仮想シナリオの（専門家間の知的体操との）意味での適切さ」です。別記事（７）「ワクチンで感染者が９割減」は誤りは、この「論文著者が意図した反実仮想シナリオの意味での適切さ」には（専門家間の知的体操として適切だとしても）一般的な意味での不適切さがある、という問題を指摘しています。

（７）結論

Sci Rep 2023 論文の年齢層別の実効再生産数 $R_{ab,t}$ が論文中のどの式で計算されたのかは、必ずしも明確ではありません。そこで $R_{ab,t}$ が論文の式(2) で計算されたとの考え方と、式(3) で計算されたとの考え方を検討しました。その結果、式(2) で計算された可能性が高いと考えられます。この場合、論文が計算している反実仮想シナリオでの実効再生産数や新規感染者数は、 $論文\ 式(3)$ にある項の不適切な値による影響を受けています。

この論文の Figure 1 のオレンジの dot と緑の line とは、「よく fit している」などと表現されることがありますが、年齢層別の実効再生産数が式(2) で計算されているなら、両者が fit しているのは計算の仕様から当然です。このグラフが fit していることは、論文の数理モデルの正当性を保証するものではありません。

本稿が検討してきた疑問に明快な回答を与えるためにも、Sci Rep 2023 論文の著者は計算プログラムを公開し、計算の詳細を検証可能にすべきです。

参考文献

[Goldberg 2021] Y. Goldberg, M. Mandel, Y. M. Bar-On, O. Bodenheimer, L. Freedman, E. J. Haas, R. Milo, S. Alroy-Preis, N. Ash, and A. Huppert, "Waning immunity after the BNT162b2 vaccine in Israel," New England Journal of Medicine, vol. 385, no. 24, Art. no. e85, Dec. 2021. [Online]. Available: https://doi.org/10.1056/nejmoa2114228.

[稲葉 2020] 稲葉寿編著, "感染症の数理モデル増補版," 培風館, 2020-12.

[Kakeya 2024] H. Kakeya, M. Itoh, Y. Kamijima, T. Nitta, and Y. Umeno, "Unreliability in Simulations of COVID-19 Cases and Deaths Based on Transmission Models," medRxiv, preprint, Feb. 2024. [Online]. Available: https://doi.org/10.1101/2024.02.02.24302123.

[Kakeya 2025] H. Kakeya and Y. Umeno, “Validation and Sensitivity Analysis of the COVID-19 Transmission Model Simulating Counterfactual Infections in Japan,” medRxiv, 2025. [Online]. Available: https://doi.org/10.1101/2025.02.08.25321916.

[Kayano 2023a] T. Kayano et al., "Evaluating the COVID-19 vaccination program in Japan, 2021 using the counterfactual reproduction number," Scientific Reports, vol. 13, no. 1, article 17762, 2023. [Online]. Available: https://doi.org/10.1038/s41598-023-44942-6.

[Kayano 2023b] T. Kayano and H. Nishiura, "Assessing the COVID-19 vaccination program during the Omicron variant (B.1.1.529) epidemic in early 2022, Tokyo," BMC Infectious Diseases, vol. 23, no. 1, p. 746, 2023. [Online]. Available: https://doi.org/10.1186/s12879-023-08748-1.

[Nakamura 2024a] T. Nakamura, "Transmission model and arithmetic of dynamical systems," ResearchGate, [Online]. Available: http://dx.doi.org/10.13140/RG.2.2.12968.99840/1. [Accessed: Dec. 21, 2024].

[Nakamura 2024b] T. Nakamura, "Remarkable data in Kayano T, Ko Y, Otani K, et al.," ResearchGate, [Online]. Available: http://dx.doi.org/10.13140/RG.2.2.22188.68489. [Accessed: Dec. 21, 2024].

[Tartof 2021] S. Y. Tartof et al., "Effectiveness of mRNA BNT162b2 COVID-19 vaccine up to 6 months in a large integrated health system in the USA: a retrospective cohort study," The Lancet, vol. 398, no. 10309, pp. 1407–1416, Oct. 2021. [Online]. Available: https://doi.org/10.1016/S0140-6736(21)02183-802183-8).

修正履歴

2025-02-19
公開。
2025-02-28
以下の修正を行いました。これによる論旨の変更はありません。
- (3-2-3-1)節で、[Goldberg 2021] と [Tartof 2021] が計算している効果を、「実質的に発症予防効果」などと記述していましたが、これを「発症予防効果に近いもの」に改めました。
- (3-2-3-4)節に式(3)説の成立に否定的な事項を書いていたのですが、説得力のない事項だったので削除しました。
2025-03-10
以下の修正を行いました。論旨に変更はありません。
- (3-2-3-3)節の「（両者が独立であること）を前提にしています。」は、「（両者が排反であること）を前提にしています。」の誤記でした。直後の「この式が妥当であるためには、」以下でこの部分を言い換えていますが、ここの修正は必要ありません。
2025-12-25
後日の検討により、本稿の主たる内容には修正すべき点があると考えるようになったので、冒頭にその旨を加筆しました。ただし、本稿 (3-2-3-1)～(3-2-3-3) が述べている、Sci Rep 2023 論文の数理モデルが含有している問題点についての考えに変わりはありません。

2025-02-19

西浦氏の Scientific Reports 論文について（８）論文が採用しているワクチン効果への疑問

「接触8割減」の問題をまとめた論考はこちらに。
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

私がネット上でしていることのまとめは、こちらに。
https://sarkov28.hatenablog.com/entry/2022/03/29/160915

（１）序論
（２）論文におけるワクチンの効果は、（発症予防効果ではなく）感染予防効果
（３）論文がワクチンの効果の根拠とした2つの論文
（４）考察
（５）結論
参考文献
修正履歴

（１）序論

図1.1　Sci Rep 2023 論文の Figure 1（本稿に Figure 1 への言及はありません。）

Sci Rep 2023 論文は、数理モデル上に反実仮想シナリオ counterfactual scenarios を作る計算手法により、ワクチンなしでの感染者数を計算したと主張しています。これに対して私はブログの別の記事で、

論文が計算している感染者数が、一般的な意味における「ワクチンなしでの感染者数」とは異なっていること。
論文が計算している感染者数は、過大であるのが分かっていること。
論文が計算している感染者数を現実の感染者数と比較し、「これがワクチンの効果である」などと述べるのは不適切であること。

を指摘しました。本稿は、この論文が使用しているワクチンの効果 vaccine efficacy の問題を検討します。

この論文は、参考文献に2つの論文を挙げ、これらを根拠としてワクチンの効果を数理モデルに組み入れています。ここで重要なのは、Sci Rep 2023 論文が使っているワクチンの効果が、感染予防効果であることです。この論文は「ワクチンが有効な状態では感染しない」としています。

本稿は、Sci Rep 2023 論文がワクチンの根拠にしている複数の論文が示すワクチンの効果が、感染予防効果ではなく、発症予防効果に近いことを示します。したがって Sci Rep 2023 論文は、不適切なワクチンの効果を用いています。

ワクチン効果の値が不適切だと、これを用いて計算する、ワクチンなしシナリオにおける実効再生産数の値が不適切になります。したがって論文が計算しているワクチンなしシナリオにおける感染者数も、不適切な値になります。

（２）節では、Sci Rep 2023 論文が数理モデルに組み込んでいるワクチンの効果が、（発症予防効果ではなく）感染予防効果であることを示します。（３）節では、論文がワクチンの効果を参照している2つの論文を示すと共に、それら論文が示しているワクチンの効果が（感染予防効果ではなく）発症予防効果に近いことを示します。（４）節では、考察を述べます。（５）節では、本稿の結論を述べます。

Sci Rep 2023 論文については、複数の記事で書いています。

（２）論文におけるワクチンの効果は、（発症予防効果ではなく）感染予防効果

Sci Rep 2023 論文は、式(1) でワクチンの効果 $l_{a,t}$ を示し、式(3) で実効再生産数 $R_{ab,t}$ とワクチンの効果との関係を示しています。

$\displaystyle l_{a,t} = \frac{1}{n_a} \sum_{s=1}^{t-1}\ v_{a,t-s}\ h_s\ \ ...\ \ 論文\ 式(1)$

$\displaystyle R_{ab,t} = \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right) K_{ab}\ p\ h_t\ d_t\ c_t\ \ ...\ \ 論文\ 式(3)$

ここで、, は年齢層、は時刻、はワクチン接種からの経過時間です。

論文式(3) の右辺最初の部分

$\displaystyle \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right)$

は、Sci Rep 2023 論文にも "which accounts for the immune fraction owing to vaccination and infections among susceptible individuals (i.e., infectees)"「感受性のある個体におけるワクチン接種および感染による免疫割合（すなわち、感受性者）を示している。」とあるように、感受性者比率です。

ここで、ワクチンの効果 $l_{a,t}$ がから差し引かれています。これはこの数理モデルが、

(ワクチンの効果がある) = (感受性人口ではない)

との考えに立っていることを示しています。

つまり、Sci Rep 2023 論文が用いているワクチンの効果 $l_{a,t}$ （ $論文\ 式(3)$ ）は、感染予防効果です。

図2.1　Sci Rep 2023 論文の式(3)

（３）論文がワクチンの効果の根拠とした2つの論文

(3-1) Sci Rep 2023 論文におけるワクチン効果の記述

Sci Rep 2023 論文に以下の記述があります。

SARS-CoV-2, all vaccinated individuals retrieved from the Vaccine Record System (VRS) were converted into immunized people according to time. [ ... ] For the conversion, we used a profile of vaccine efficacy involving waning immunity for the primary series used by Gavish et al.19, which was based on previous estimates 53, 54.

SARS-CoV-2 で、ワクチン記録システム（VRS）から取得されたすべてのワクチン接種者は、時間経過に応じて免疫を獲得した人々に変換された。（略）この変換には、Gavish et al. 19 が使用した一次シリーズに関する免疫減衰を含むワクチンの有効性のプロファイルを使用した。これは、以前の推定値に基づいている 53, 54

Sci Rep 2023 論文の参考文献 19 は [Gavish 2022]、53 は [Goldberg 2021]、54 は [Tartof 2021] です。次節以降で、[Goldberg 2021] と [Tartof 2021] がワクチンの効果をどのように記述しているのかを見ていきます。

(3-2) [Goldberg 2021] が調べているワクチンの効果

[Goldberg 2021] は、研究に使用したデータを以下のように説明しています。

We used data on confirmed infection and severe disease collected from an Israeli national database for the period of July 11 to 31, 2021, for all Israeli residents who had been fully vaccinated before June 2021.

2021年6月以前に完全にワクチン接種を受けたすべてのイスラエル居住者を対象として、2021年7月11日から31日までの期間にイスラエルの全国データベースで収集された、確認された感染および重症疾患に関するデータを使用した。

このデータには「発症して医師の診断を受け、検査で陽性になった人の割合が、市中よりも多い」という偏りがあると思われます。感染しても症状が無かったり軽微だったりすれば、受診しないために登録されなかった人がいるでしょう。

[Goldberg 2021] はこのようなデータベースの感染者を調べ、ワクチンの効果を計算しています [注3-2a]。

[注3-2a] [Goldberg 2021] は、データにあるバイアスを解消するための調整を試みていますが、ここで私が問題視している、「発症し、受診し、検査陽性になった人が多い」というバイアスの解消は試みられていません。

(3-3) [Tartof 2021] が調べているワクチンの効果

[Tartof 2021] は、研究に用いたデータについて以下のように述べています。

In this retrospective cohort study, we analysed electronic health records from the Kaiser Permanente Southern California (KPSC) health-care system (CA, USA) to assess the effectiveness of the BNT162b2 vaccine against SARS-CoV-2 infections and COVID-19-related hospital admissions. [ ... ] KPSC electronic health records integrate clinical data including diagnostic, pharmacy, laboratory, and vaccination history information across all settings of care. Care delivered to members outside of the KPSC system is also captured, as outside providers must submit detailed claims to KPSC for reimbursement by the health plan.

この後ろ向きコホート研究において、私たちはカリフォルニア州の Kaiser Permanente Southern California（KPSC）医療システムの電子健康記録を分析し、BNT162b2 ワクチンの SARS-CoV-2 感染および COVID-19 関連の入院に対する有効性を評価した。（略）KPSC の電子健康記録は、診断、薬局、検査、ワクチン接種履歴を含む臨床データを、すべての医療提供環境にわたって統合している。また、KPSC システム外で会員に提供された医療も記録されており、外部の医療提供者は健康保険の払い戻しのために KPSC に詳細な請求を提出する必要がある。

KPSC 医療システムのデータには「発症して医師の診断を受け、検査で陽性になった人」の割合が、市中よりも多いと思われます。このデータベースには、ドライブスルー検査のデータも入っていますが、それでも「検査に行く人」は「市中の人」のランダムなサンプルではありません。

[Tartof 2021] が計算したワクチンの効果は、このようなデータに基づいています [注3-3a]。

[注3-3a] [Tartof 2021] は、データにあるバイアスを解消するための調整を試みていますが、ここで私が問題視している、「発症し、受診し、検査陽性になった人が多い」というバイアスの解消は試みられていません。

（４）考察

（２）節で検討したように、Sci Rep 2023 論文で用いられているワクチンの効果 vaccine efficacy は、論文の式(1)、式(3) によれば（発症予防効果ではなく）感染予防効果です。感染予防効果でないものを用いたら、論文式(3) が成立しなくなります。

ところが（３）節で検討したように、Sci Rep 2023 論文がワクチン効果を参照している論文、[Goldberg 2021] と [Tartof 2021] が計算に使っているのは、感染者ではなく、発症者に近いものでした。したがって、これらの論文が調べているのは正確な意味での感染予防効果ではなく発症予防効果に近いものになります。

この結果、論文式(3) は不適切な値を含んだ式になっています。したがって、この式を使って実効再生産数 $R_{ab,t}$ を計算すると不適切な値になります。

確認しておきますが本稿は、[Goldberg 2021] や [Tartof 2021] のデータ処理の不適切さを指摘しているのではありません。これらの論文は、データにバイアスがあることを認識し、可能な範囲でその除去や低減に努めています。また、データに残余しているバイアスへの留意を促しています。

しかし、これらの論文は、本稿が問題にしている「データが、発症し、受診し、検査陽性になった人に偏る」というバイアスを解消できていません。このバイアスの解消は、実質的に不可能だと思われます。なぜならこれを解消するためには、「日次の、無症状者を含めた正確な感染者数のデータ」が必要ですが、新型コロナ感染症でこれを調べるためには検査対象者全員を毎日検査するなどの非現実的な調査が必要になるからです。

（５）結論

Sci Rep 2023 論文は、反実仮想シナリオ counterfactual scenarios を用いてワクチンなしの場合の感染者数を計算する際、ワクチンの効果 vaccine efficacy として正確な意味での感染予防効果を用いています。ところが論文がワクチンの効果を引用している参考文献 [Goldberg 2021] と [Tartof 2021] が示しているのは感染予防効果ではなく、発症予防効果に近いものでした。

Sci Rep 2023 論文は、ワクチンの効果として不適切な数値を用いています。このため、論文式(3) は不適切な実効再生産数 $R_{ab,t}$ を計算しています。したがってこの論文が計算する、ワクチンなしシナリオなどでの感染者数は、不適切な値になっています。

参考文献

[Gavish 2022] N. Gavish, R. Yaari, A. Huppert, and G. Katriel, "Population-level implications of the Israeli booster campaign to curtail COVID-19 resurgence," Sci. Transl. Med., vol. 14, no. 647, abn9836, 2022, [Online]. Available: https://doi.org/10.1126/scitranslmed.abn9836.

[Kayano 2023] T. Kayano et al., "Evaluating the COVID-19 vaccination program in Japan, 2021 using the counterfactual reproduction number," Scientific Reports, vol. 13, no. 1, article 17762, 2023. [Online]. Available: https://doi.org/10.1038/s41598-023-44942-6.

修正履歴

2025-02-19
公開。
2025-02-28
[Goldberg 2021] と [Tartof 2021] が計算しているワクチンの効果を「実質的に発症予防効果」と書いていましたが、「発症予防効果に近い」に改めました。論旨の変更はありません。

2024-12-17

西浦氏の Scientific Reports 論文について（７）「ワクチンで感染者が９割減」は誤り

「接触8割減」の問題をまとめた論考はこちらに。
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

私がネット上でしていることのまとめは、こちらに。
https://sarkov28.hatenablog.com/entry/2022/03/29/160915

（１）序論
（２）雨と傘の例え
（３）論文の感染者数と現実の感染者数を比較する誤り
（４）ワクチンなしシナリオの不自然さは解消できない
- (4-1) ワクチンなしシナリオの不自然さは解消できない
- (4-2) 実効再生産数を変更した計算
（５）ワクチンなしシナリオの不自然さを示す、Sci Rep 2023 論文の記述
- (5-1) 説明の準備
- (5-2) ワクチンなしシナリオの不自然さを示す、Sci Rep 2023 論文の記述
（６）「論文の感染者数と現実の感染者数を比較する誤り」の例
（７）Sci Rep 2023 論文について述べた西浦氏の投稿の検討
（８）Sci Rep 2023 論文の意義の再検討
- (8-1) Sci Rep 2023 論文の計算結果が政策判断の助けになるかは疑問
- (8-2) 一般の人にとって Sci Rep 2023 論文とは
（９）論文への誤解の原因と西浦氏の責任
- (9-1) Sci Rep 2023 論文の説明不足と、それによる誤解の拡散
- (9-2) 西浦氏が説明すべきこと
（１０）政府や企業の対策に関するシナリオの問題点
（１１）[Kayano 2023b] における、Sci Rep 2023 論文と同じ構造の問題
（１２）結論
（参考文献）
（付録）
- (付録Ａ) 本稿に関係のある url など
- (付録Ｂ) 本稿に出てくる url とアーカイブ
（更新履歴）

（１）序論

図1.1　Sci Rep 2023 論文の Figure 1（本稿の Figure 1 への言及は、限定的です。）

西浦氏は、同時期に東京のオミクロン流行時に関する論文 [Kayano 2023b] も発表しました。[Kakeya 2024] は、これらの論文におけるパラメータの信頼性の低さや、クロスバリデーションや現実データとの整合性の検証の不足を指摘しています。[Nakamura 2024a] は、[Kayano 2023b] の数理モデルに数学的不正確さなどの問題を示しています。[Nakamura 2024b] は、[Kayano 2023a] の結果の不自然さなどを述べています。[Kakeya 2024]、[Nakamura 2024a]、[Nakamura 2024b] は、Sci Rep 2023 論文や [Kayano 2023b] についての疑問の検証のために、ソースコードの開示が必要なことを指摘しています。本稿は、Sci Rep 2023 論文の計算の前提や方法を受け入れた上で、その前提や方法に内在する限界と誤解の存在を指摘します。またこの誤解に関する誤りが社会に広がっていることを指摘します。

Sci Rep 2023 論文を引用してワクチンの効果を述べた説明には、しばしば誤りがあります。「論文のワクチンなしシナリオでの推定感染者数と、現実の感染者数とを比較し、それをワクチンの効果のように語ること」は誤りです。３つの学会（日本感染症学会、日本呼吸器学会、日本ワクチン学会）が連名で発表した見解が Sci Rep 2023 論文に言及した部分は、この誤りに陥っています。

これは Sci Rep 2023 論文に関する典型的な誤りでもあるので、本稿は、これが誤りであることを説明します。同様の誤りが、西浦氏の SNS 投稿や産経記事、Sci Rep 2023 論文にあることも示します。この論文は、非常に特殊なシナリオでの感染状況を計算しています。このシナリオは不自然で非現実的なものです。計算結果は現実に起きる可能性がないものであり、また過大であることが分かっています。

（２）節では、例えを用いて論文のシナリオが不自然で非現実的であること、計算結果の感染者数が過大であることを示します。（３）節では、「論文の感染者数と現実の感染者数を比較する誤り」を示し、この誤りが生まれる背景を検討します。（４）節では、ワクチンなしシナリオの不自然さが解消不可能であることを示します。（５）節では、ワクチンなしシナリオの不自然さを、この論文も実質的に説明していることを示します。（６）節では、（３）節の誤りの実例として、Sci Rep 2023 論文、西浦氏の x.com への投稿、産経記事、３つの学会の見解、における誤りを説明します。（７）節では、論文について述べた西浦氏のスレッドを検討します。（８）節では、論文の意義について再検討します。（９）節では、論文への誤解の原因と、西浦氏の責任について検討します。（１０）節では、政府や企業の対策に関するこの論文の問題点を述べます。（１１）節では、[Kayano 2023b] にも Sci Rep 2023 論文と同様の問題があることを説明します。（１２）節では、結論を述べます。

この論文については、複数の記事で書いています。

（記事（７）と記事（１）とは重なる事項を検討しているため、一部に重複があります。）

（２）雨と傘の例え

（２）節では、「雨と傘の例え」を用いて、この論文のシナリオが不自然で非現実的であることを説明します。

(2-1) 雨と傘の例えの対応表と Sci Rep 2023 論文のシナリオ

Sci Rep 2023 論文の「ワクチンなしシナリオ」は、感染が現実より大幅に拡大しても、人々が行動を変えないという非現実的な想定に基づいています。本節では、このシナリオの不自然さを「雨と傘の例え」を用いて説明します。

この例えでは、感染症の状況を「雨の強さ」、感染症への感染を「雨にかなり濡れること」、ワクチンによる感染予防効果を「傘」、個人の感染予防行動を「雨を避ける行動」に例えます [注2-1a]。

表2-1 「雨と傘の例え」の対応表

コロナとワクチンの状況	雨と傘の例え
コロナの状況	雨の強さ
現実（ワクチンあり）　でのコロナの状況	小雨
ワクチンなし　でのコロナの状況	大雨
コロナへの感染	雨にかなり濡れること
ワクチンによる感染予防効果	傘
ワクチン以外の個人の感染予防行動	雨を避ける行動（外出を控える、　移動手段を工夫するなど）

この例えは、雨にかなり濡れた人が増加した理由が1つ（「傘がなくなったこと」）ではなく、2つ（「傘がなくなったこと」と「不自然な行動をしたこと」）であることを確認するために示しています。これが確認できると、「論文のワクチンなしシナリオの想定の非現実性」や「計算される感染者数が過大であること」が確認できます。

ワクチンあり（傘あり）の現実的シナリオでのある日は、「雨と傘の例え」では以下になります。

小雨で（コロナの状況が現実と同じで）、６割の人が傘を差しています（ワクチンによる免疫を持っています）。傘を持っていない人（ワクチンによる免疫がない人）も４割いて、その人たちは雨を避けます（感染を避けます）が、一部の人は、雨にかなり濡れました（感染しました）。

ここでの人々の行動に不自然なところはありません。（ワクチンによる免疫を持つ人が６割の状況を想定しています。）

ワクチンなし（傘なし）の反実仮想シナリオでの同じ日は、Sci Rep 2023 論文の考え方では以下になります。

大雨で（コロナが大幅に（現実の１０倍以上に）拡大した状況で）、傘を差している人（ワクチンによる免疫がある人）は一人もいません。しかし６割の人は、傘を持っている時と同じ行動をする（行動を変えない）ので、雨にかなり濡れる人（感染する人）がいました。また、４割の人は雨を避けますが（感染を避けますが）、その避け方は、大雨が降っているのに小雨が降っている時と同じなので（感染が大幅に拡大した状況なのに現実と同じなので）、雨にかなり濡れる人（感染する人）がいました。

ここでの人々の行動は不自然です。状況が（雨が、感染状況が）変わっているのに行動を変えないからです。

ワクチンなし（傘なし）シナリオでの人々の行動は不自然です。Sci Rep 2023 論文はこの不自然な状況で感染者数（雨にかなり濡れた人数）を数えているので、この論文が計算する感染者数は不自然な値になります。

この例えには限界があります。この例えで考えても、雨にかなり濡れた人の増加が、2つの理由（「傘がなくなったこと」と「不自然な行動をしたこと」）のどちらにどの程度起因するのかを判断することはできません。したがってどちらが主因なのかを検討することもできません。この例えで行えるのは、雨にかなり濡れた人が増加した理由が1つ（「傘がなくなったこと」）ではなく、2つである、ということの確認です。

またこの例えは、いわゆる感染症の従属性は表現できません。例えが「ある日の」などと時間を区切っているのはこの点に対応するためです。「ある日の」と時間を区切ってもこの例えの目的に影響はありません。ある日のワクチンなしシナリオが不自然で非現実的であることが示せれば、この例えの目的は済んでいます。

[注2-1a] Sci Rep 2023 論文は、ワクチンを接種すると（時間が経過すると減衰するが）感染予防効果を得られるという考え方を採っています [注2-1b]。またこの論文は、人々の行動の変化が実効再生産数に影響を与えると考えています [注2-1c]。本稿はこれらの考え方で考えます。本稿が、「Sci Rep 2023 論文と同様に考えた場合の問題点を検討する」という方針だからです。
[注2-1b] Sci Rep 2023 論文は、式(1) で計算したワクチンの効果 $l_{a,t}$ を式(3) で使っています。式(1) の計算結果は、補足情報（41598_2023_44942_MOESM1_ESM.docx）の Supplementary Figure S2 に示されています。
[注2-1c] Sci Rep 2023 論文は、人々の活動度 h_t を式(4) で計算し、式(3) で使っています。関連するグラフとして、補足情報（41598_2023_44942_MOESM1_ESM.docx）の Supplementary Figure S4 があります。

(2-2) ワクチンなしシナリオの感染者数は過大

Sci Rep 2023 論文の「ワクチンなしシナリオ」では、感染が現実より大幅に拡大しても、人々の行動が変わらないと想定しています。この非現実的な想定によって、推定される感染者数が過大になっています。本節では、このシナリオの感染者数が過大である理由を「雨と傘の例え」を用いて説明します。

(2-1)節で示したように、ワクチンなし（傘なし）シナリオでの人々の行動は以下でした。

「雨と傘の例え」で考えると：

６割の人は大雨で傘を持っていないのに、小雨で傘を持っていた時と同じ行動をする。
４割の人の雨の避け方は（大雨が降っているのに）小雨が降っている時と同じである。

コロナとワクチンで考えると：

６割の人はコロナが大幅に拡大してワクチンによる免疫がないのに、現実の感染状況でワクチンによる免疫がある時と同じ行動をする。
４割の人の感染の避け方は（コロナが大幅に拡大した状況なのに）現実の感染状況の時と同じである。

ここには不自然な行動があります。この状況で増えた感染者数（雨にかなり濡れた人数）には、不自然な行動を原因とする人数が含まれています。したがって、ワクチンなしシナリオでの感染者数は過大になっています。このことは、論文の限界事項（limitations）に記載されるべきですが、論文にその記述はないので不適切です。

Sci Rep 2023 論文のワクチンなしシナリオでの感染者数が過大だとしても、それがどの程度過大なのかは不明です。どの程度過大なのかを計算するためには、（４）節で検討する「人々が感染拡大に対してどう行動を変えるかの予測」と「その行動変化による実効再生産数の変化の数値的な予測」が必要です。これらを予測する方法は実質的にないので、この論文の感染者数がどの程度過大なのかを計算することはできません。

(2-3) 感染者数と死者数での同じ問題の発生

Sci Rep 2023 論文では、感染者数に IFR（感染者致死率）を乗じて死者数を計算しています。この計算は、年齢層ごとに行われ、各年齢層の死者数は、その年齢層の感染者数に比例します。ただし、全年齢層の死者数は、全年齢層の感染者数に比例はしません。年齢層ごとにIFRが異なるためです。

年齢層ごとの死者数はその年齢層の感染者数に比例するので、各年齢層の感染者数で起きた（(2-2)節で論じた過大さのような）な問題は、死者数でも同様に生じます。この関係は各年齢層で成立するので、全年齢層での感染者数と死者数でも同様の問題が生じます。

本稿は感染者数や死者数の具体的な数値の正確性を論じるものではなく、計算における構造的な問題を指摘しようとしています。このため、年齢層ごとの詳細な議論を省略しても、指摘している問題の妥当性に影響はありません。

また本稿は、主に感染者数の問題を議論しますが、Sci Rep 2023 論文の計算方法では、感染者数と死者数で同じ問題が成立します。感染者数が過大ならば死者数も同様に過大です。感染者数がどの程度過大なのかが不明であれば、死者数がどの程度過大なのかも不明です。

(2-4) 本稿への疑問に(1) 論文の「反実仮想 counterfactual シナリオ」は非現実的

(2-1)節に対し、以下のような疑問があるかも知れません。

(2-1)節は、Sci Rep 2023 論文のワクチンなしシナリオが非現実的などと説明している。しかしもともと論文は、ワクチンなしシナリオを「反実仮想 counterfactual シナリオ」と記述している。(2-1)節の指摘は論文の意図を説明しているだけでは。当たり前のことを述べているだけでは。

確かに論文は、ワクチンなしシナリオなどを反実仮想シナリオと記述しています。しかし、(2-1)節が示しているのは、これが単なる「事実と異なるシナリオ」ではなく、「現実性が全くないシナリオ」だということです。

図2.1 は、「シナリオ全体の集合」を3つの集合

「現実的なシナリオの集合」
「現実性が乏しいシナリオの集合」
「現実性が全くないシナリオの集合」

に分け、これらの集合に属する要素である

「（ワクチン接種があった）現実」
「現実社会にワクチンがなかったら、どうなっていたのかのシナリオ」
「論文のワクチンなしシナリオ」

を、(2-1)節～(2-3)節の考え方で配置したものです。

図2.1　3つのシナリオの、3つの集合における位置

論文の「反実仮想シナリオ」である「ワクチンなしシナリオ」は、(2-1)節に示したように非現実的なシナリオです。このシナリオの非現実性は、「たまたま現実とは違うが、偶然が重なれば現実がこうでもおかしくない」（＝現実的なシナリオ）や「現実性は乏しいが、もしかしたらこういうことがあるかも知れない」（＝現実性が乏しいシナリオ）における非現実性とは異なります。

「ワクチンなしシナリオ」の非現実性は、現実性が全くないという非現実性です。この非現実性は、論文では明確になっていませんでしたが、(2-1)節は、このことを明確に示しました。したがって、本節冒頭に示した「(2-1)節が論文の意図を説明しているだけでは」との疑問は、妥当ではありません。

(2-5) 本稿への疑問に(2) 論文は「全ての行動が変わらない」を実質的に前提している

(2-1)節に対し、以下のような別の疑問があるかも知れません。

(2-1)節は、Sci Rep 2023 論文の「ワクチンなしシナリオ」が「状況が変化しても、全ての行動が変わらない」を前提しているかのように述べている。しかしそのような前提は論文に記載がない。(2-1)節は、勝手な前提を作り上げてそれを批判しているのでは。

説明が長くなるので上では書きませんでしたが、その疑問は次のように考えれば解決します。

「状況が変化しても、行動が変わらない」は、「状況が変化しても、実効再生産数に影響を与える行動変容はない」を意味している。

状況が変化した時の人々の行動を、「実効再生産数に影響を与える行動」と「実効再生産数に影響を与えない行動」に分けます。後者の影響を与えない行動は、実効再生産数に影響を与えないのですから、論文や本稿が考慮する対象から除外しても論旨に影響を与えません。

一方前者について論文は、「状況が変化しても、実効再生産数に影響を与える行動変容はない」を前提しています。これは論文の式(3)から分かります。Sci Rep 2023 論文でワクチンに関する状況を変化させるのに用いているのは式(3)です。

$\displaystyle R_{ab,t} = \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right) K_{ab}\ p\ h_t\ d_t\ c_t\ \ ...\ \ 論文\ 式(3)$

論文は、「ワクチンありの現実的シナリオ」「ワクチンなしの反実仮想シナリオ」のどちらでも、論文式(3) が成立すると主張しています。もしも「（ワクチンに関する）状況が変化したら、実効再生産数に影響を与える行動変容がある」と論文が前提しているなら、これに該当する項が論文式(3)の右辺に必要です。その項がないとワクチンなしのシナリオの時に等式が成立しなくなるからです。しかしそのような項は式(3)の右辺に存在しません。

したがって論文は式(3)で、「状況が変化しても、実効再生産数に影響を与える行動変容はない」と述べています。

したがって本節冒頭に示した「(2-1)節は勝手な前提を作り上げてそれを批判しているのでは」との疑問は、妥当ではありません。

（３）論文の感染者数と現実の感染者数を比較する誤り

(3-1) ワクチンなしシナリオについての誤った印象

「ワクチンを接種していないシナリオ」と聞くと、つい「ワクチンを接種しない想定だが、そこでの人々の行動は、常識的で自然なものを想定したシナリオ」だと考えてしまうかも知れません。しかし、それは誤解です。

Sci Rep 2023 論文のシナリオはそうした現実的なものではありません。この論文のワクチンなしシナリオは、(2-1)節で述べたように「ワクチンを接種しない想定だが、感染が現実より大幅に拡大しているにもかかわらず、人々が行動を変えないというシナリオ」です。

この論文が想定しているワクチンなしシナリオが、このように不自然で非現実的なものになる直接の原因は、論文の「状況が大きく変化しても人々は行動を変えない」との想定が不自然で非現実的だからです。

(3-2) 感染者数比較の誤り：本来あるべき比較

Sci Rep 2023 論文のように「ワクチン接種で感染予防効果が得られる」と考えるなら、

疑問〈3-2a〉
「この社会にもしワクチンがなかったら、感染者数や死者数はどうなっていたのか」

という疑問が出てくるのは自然です。しかしこの論文の推定感染者数は、この疑問への回答になりません。

表3-2-1 は、疑問〈3-2a〉に回答するための、本来の比較です。

表3-2-1 「この社会にもしワクチンがなかったら、感染者数や死者数はどうなっていたのか」のための比較

	ワクチンあり	ワクチンなし
ワクチン	あり	なし
状況が変化した時の人々の行動指針	状況に応じて柔軟に行動を変える	状況に応じて柔軟に行動を変える

ワクチンなしでの感染者数と現実の感染者数を比較するなら、この比較を行う必要があります。

状況に応じて行動が変わるのが自然な人間の姿です。状況が変わっても行動が変わらないのは不自然です。表3-2-1 の左右で違うのはワクチンの有無だけなので、この左右での感染者数を比較すれば、疑問〈3-2a〉への答えになると期待できます。

一方、Sci Rep 2023 論文の推定感染者数を使った比較は、以下になります。

表3-2-2 Sci Rep 2023 論文を使った比較

	ワクチンあり	ワクチンなし
ワクチン	あり	なし
状況が変化した時の人々の行動指針	状況に応じて柔軟に行動を変える	状況が変化しても行動を変えない

Sci Rep 2023 論文が計算した感染者数と現実の感染者数の比較は、この比較になります。

「Sci Rep 2023 論文を使った比較」のワクチンなしシナリオは、状況が変化しても（感染状況が現実の１０倍以上に拡大しても）人々の行動は変化しないシナリオです。これは人間の行動にあるはずの性質を欠いた奇妙なシナリオです。そして「Sci Rep 2023 論文を使った比較」では、ワクチンの有無だけでなく、状況が変化した時の人々の行動の方針も異なります。この条件で感染者数を比較しても、疑問〈3-2a〉への答えにはなりません。

以上の検討により、

疑問〈3-2a〉
「この社会にもしワクチンがなかったら、感染者数や死者数はどうなっていたのか」

という自然な疑問に回答するための比較として、「Sci Rep 2023 論文を使った比較」が間違いであることが分かります。論文の推定感染者数と現実の感染者数の比較（表3-2-2）では、疑問〈3-2a〉への答えにはなりません。比較として適切なのは、本来の比較（表3-2-1）です。

(3-3) Sci Rep 2023 論文が答えている疑問とは

(3-2)節での検討は、自然な疑問である

疑問〈3-2a〉
「この社会にもしワクチンがなかったら、感染者数や死者数はどうなっていたのか」

との疑問に Sci Rep 2023 論文が答えていないことを示しています。「Sci Rep 2023 論文を使った比較（表3-2-2）」ではこの疑問に回答できないからです。

一方で、この論文が答えている疑問（＝「Sci Rep 2023 論文を使った比較（表3-2-2）」が答えられる疑問）は以下です。

疑問〈3-3a〉
「感染規模が現実の１０倍以上に拡大しても現実と同じ行動をする、との不自然な社会に、もしワクチンがなかったら、感染者数や死者数はどうなっていたのか」

これは、疑問〈3-2a〉とは全く違う疑問です。Sci Rep 2023 論文は、ほとんどの人が問わない疑問（疑問〈3-3a〉）に答えています。そして、自然な疑問（疑問〈3-2a〉）に答えていると誤解されています。

Sci Rep 2023 論文が計算しているのは、現実の社会のワクチンの効果ではなく、不自然な社会でのワクチンの効果です。

(3-4) 感染者数比較の誤り：例えによる説明

(3-2)節・(3-3)節での検討と重なる内容を、例えを用いて説明します。（ここまでで納得した方は読む必要がないかもしれません。）

「雨と傘の例え」における、傘ありシナリオで雨にかなり濡れた人数と、傘なしシナリオで雨にかなり濡れた人数とを比較して、「これが傘の効果です」と述べるのは誤りです。

傘なしシナリオで雨にかなり濡れた人が増加したのは、傘がなかったことが原因の一つです。しかし、それだけではありません。６割の人が、大雨で傘を持っていないのに、小雨で傘を持っていたときと同じ行動をしたことも原因です [注3-4a]。
雨にかなり濡れた人の増加が、傘がなかったことが原因であるかのように（あるいはそれが主因であるかのように）述べるのは誤りです。雨にかなり濡れた人数を両者で（傘ありシナリオと、傘なしシナリオとで）比較して、それを傘の効果だと示すことはできません。傘の他にも理由があるからです。

同様に、現実の推定感染者数と、ワクチンなしシナリオでの推定感染者数とを比較して、「これがワクチンの効果です」と述べるのは誤りです。
ワクチンなしシナリオで感染者数が増加したのは、ワクチンによる免疫がなかったことが原因の一つです。しかし、それだけではありません。６割の人が、感染が大幅に拡大した中でワクチンによる免疫がないのに、現実の感染状況でワクチンによる免疫があったときと同じ行動をしたことも原因です [注3-4b]。
感染者の増加が、ワクチンによる免疫がなかったことが原因であるかのように（あるいはそれが主因であるかのように）述べるのは誤りです。推定感染者数を両者で（現実とワクチンなしシナリオとで）比較して、それをワクチンの効果だと示すことはできません。ワクチンの他にも理由があるからです。

[注3-4a] 雨にかなり濡れた人が増加した原因には、４割の人の不自然な行動（大雨なのに小雨の時と同じ行動をした）もあります。
[注3-4b] 感染者数が増加した原因には、４割の人の不自然な行動（感染が大幅に拡大しているのに現実と同じ行動をした）もあります。

(3-5) 論文の感染者数と現実の感染者数を比較する誤り

(3-2)節～(3-4)節での検討を踏まえて、Sci Rep 2023 論文に関してしばしば見られる誤りを確認します。

〈3-5a〉論文の感染者数と現実の感染者数を比較する誤り
Sci Rep 2023 論文のワクチンなしでの推定感染者数と、現実の推定感染者数とを比較して、「これがワクチンの効果です」と述べるのは誤りです。

この論文を根拠としたワクチンの効果が各所で述べられているのですが、それはしばしば、この誤りに陥っています。

この誤りの実例は、（６）節で示します。

なお、〈3-5a〉で、「現実の感染者数」ではなく「現実の推定感染者数」と書いたのは、以下の理由からです。Sci Rep 2023 論文は、全体の感染者のうち一部だけが報告されていると考えていて、その比率を感染者報告率 reporting coverage としています。論文でのこのパラメータの主な値は、0.25 です。この場合、報告感染者数を 0.25 で割り算して全体の感染者数を推定します。論文のワクチンなしでの推定感染者数と比較されているのは、報告感染者数そのものではなく、この 0.25 で割り算した値です。これは推定値なので、「現実の感染者数」ではなく「現実の推定感染者数」と書いています。

（４）ワクチンなしシナリオの不自然さは解消できない

(4-1) ワクチンなしシナリオの不自然さは解消できない

ワクチンなしシナリオに「ワクチンなしでも行動を変えない」という不自然なところがあるなら、不自然さを取り除いたシナリオにすればいいと考える人がいるかもしれません。しかし残念ながら、この不自然さを取り除くことはできません。

この不自然さを取り除くためには、「ワクチンなしシナリオで感染拡大した時には人々が行動を変える」とのシナリオで感染者数を計算することになります。このシナリオで感染者数を計算するには、人々が感染拡大に対してどう行動を変えるかを予測した上で、その行動変化による実効再生産数の変化を数値的に予測する必要があります。

これらの予測は現在のところ実質的に不可能です。（これらを予測しようとの試みはあるかも知れませんが、Sci Rep 2023 論文が不自然さを取り除いたシナリオを作成できるような成果は得られていません。）論文が「ワクチンなしでも行動を変えない」という不自然な想定を採用したのは、これが理由だと思われます。

同じことですが、ワクチンなしシナリオには、ワクチンを接種しなかった場合に現実の社会がどうなるかをモデル化しようとの意図は最初からなかったはずです。これが不可能であることは、西浦氏らには分かっていたはずだからです。現在の理論疫学ではそのようなモデル化はできないので（他のシナリオを作る方法がないので）、西浦氏は不自然で非現実的な想定のシナリオを作成し、そこでの感染者数を計算したと思われます。

(4-2) 実効再生産数を変更した計算

(4-1)節でワクチンなしシナリオの不自然さを解消できなかった一つの要因は、「行動の変化がどのように実効再生産数の変化」に結びつくかが不明だから」でした。この不明な部分を回避した、「実効再生産数が変化したら」というシナリオならば作成できます。そしてこのシナリオでの感染者数は計算できます。

つまり、「〇月〇日～〇月〇日で、実効再生産数が 0.5 下がったら」あるいは「実効再生産数が 0.5 倍になったら」などのシナリオです。

しかしこのように作成したシナリオが、実際の感染症対策に有効であるとは考えにくいです。なぜなら、これらのシナリオが前提とする「実効再生産数を 0.5 下げる（0.5 倍にする）」という感染症対策が具体的に何なのかは、不明だからです。（特定の感染症対策が実効再生産数にどのような影響を与えるのかを定量することもできません。）このように「実効再生産数を 0.5 下がったら（0.5 倍になったら）」というシナリオには別の問題が発生するので、本質的な解決になりません。

（５）ワクチンなしシナリオの不自然さを示す、Sci Rep 2023 論文の記述

「雨と傘の例え」で、ワクチンなしシナリオが不自然であることを示しました。しかし納得していない方がいるかも知れません。「そんな結論になるのは「雨と傘の例え」におかしなところがあるからではないか」と。

そうした疑問に答えるため、西浦氏が実質的に同じ内容を Sci Rep 2023 論文で述べていることを説明します。なお、ここで示すことと同じ内容を、西浦氏は x.com への投稿でも述べていますが、この投稿については後の (7-3)節で述べます。

(5-1) 説明の準備

説明のために確認しておくことがあります。
Sci Rep 2023 論文のワクチンなしシナリオが不自然なシナリオになるのは、このシナリオが「他の条件は全て同一で、ワクチン接種率だけをゼロにしたシナリオである」からです。この「他の条件が全て同一で」という部分が、「コロナ感染が大幅に（実際の１０倍以上に）拡大した状況でも、同じ行動をする」という不自然さに現れます。

したがって、

〈5-1a〉ワクチンなしシナリオは、他の条件は全て同一で、ワクチン接種率だけをゼロにしたシナリオである。

を示せば、

〈5-1b〉Sci Rep 2023 論文のワクチンなしシナリオは不自然な想定のシナリオである。

を示したことになります。

(5-2) ワクチンなしシナリオの不自然さを示す、Sci Rep 2023 論文の記述

（この (5-2)節は本文中に数式が入りますが、数式部分を飛ばして読んでも大きな影響はないようにしています。）
Sci Rep 2023 論文の式(1) と式(3) は以下です。

$\displaystyle l_{a,t} = \frac{1}{n_a} \sum_{s=1}^{t-1}\ v_{a,t-s}\ h_s\ \ ...\ \ 論文\ 式(1)$

$\displaystyle R_{ab,t} = \left( 1 - l_{a,t} - \frac{\sum_{k=1}^{t-1} i_{a,k}}{n_a} \right) K_{ab}\ p\ h_t\ d_t\ c_t\ \ ...\ \ 論文\ 式(3)$

式(1) の $v_{a,t}$ は年齢層、時刻のワクチン接種者数です。（" $v_{a,t}$ denotes the number of vaccinated individuals in age group a at calendar time t,"）ワクチンなしシナリオではワクチン接種者がいないと考えるのですから、 $v_{a,t}$ は、全ての a、t において $v_{a,t} = 0$ になります。すると式(1) から、この場合の $l_{a,t}$ は、全ての a、t において $l_{a,t} = 0$ になります。

したがって、式(3) のうち $l_{a,t}$ は常にになります。他の変数の値は変化しません。 これは、〈5-1a〉の 「他の条件が全て同一で、ワクチン接種率だけをゼロにしたシナリオ」 を、数式で表現したものです。「他の条件が全て同一」が「他の変数の値は変化しない」に対応し、「ワクチン接種率だけをゼロ」が「 $l_{a,t}$ は常に」に対応しています。

つまり Sci Rep 2023 論文は、〈5-1a〉を述べています。

〈5-1a〉ワクチンなしシナリオは、他の条件は全て同一で、ワクチン接種率だけをゼロにしたシナリオである。

論文は〈5-1a〉を述べているのですから、(5-1)節で準備したように、〈5-1b〉を述べていることになります。

〈5-1b〉Sci Rep 2023 論文のワクチンなしシナリオは不自然な想定のシナリオである。

（６）「論文の感染者数と現実の感染者数を比較する誤り」の例

Sci Rep 2023 論文は誤解されやすい論文です。実際、日本社会に広がったのは (3-5)節に示した誤り〈3-5a〉でした。

〈3-5a〉論文の感染者数と現実の感染者数を比較する誤り
Sci Rep 2023 論文のワクチンなしでの推定感染者数と、現実の推定感染者数とを比較して、「これがワクチンの効果です」と述べるのは誤りです。

（６）節では、この誤りの具体例を取り上げます。

(6-1)節：Sci Rep 2023 論文におけるこの誤りについて検討します。
(6-2)節：西浦氏の x.com への投稿におけるこの誤りについて検討します。
(6-3)節：産経新聞の記事に、この誤りがあることを示します。
(6-4)節：西浦氏によるその記事の紹介が不適切であることを説明します。
(6-5)節：日本感染症学会、日本呼吸器学会、日本ワクチン学会の見解に含まれるこの誤りを指摘します。

(6-1) Sci Rep 2023 論文における誤り

Sci Rep 2023 論文の中に、「論文の感染者数と現実の感染者数を比較する誤り」に該当する記述があります。二つを挙げます。

In the absence of vaccination, the cumulative numbers of infections and deaths during the study period were estimated to be 63.3 million (95% confidence interval [CI] 63.2–63.6) and 364,000 (95% CI 363–366), respectively; the actual numbers of infections and deaths were 4.7 million and 10,000, respectively.
（ワクチン接種を実施しなかった場合、調査期間中の累積感染者数は6,330万人（95％信頼区間［CI］63.2-63.6）、死亡者数は36万4,000人（95％CI 363-366）と推定されたが、実際の感染者数は470万人、死亡者数は1万人であった。）

A critical take-home message from the present study is that the indirect effect of vaccination was enormous in Japan. The numbers of prevented infections and deaths were 13.5 and 36.4 times the empirically observed counts, respectively.
（本研究から得られる重要な結論は、日本におけるワクチンの間接効果が非常に大きかったという点である。予防された感染者数と死亡者数は、それぞれ実測値の13.5倍と36.4倍に達した。）

どちらも論文の推定感染者数を実際の感染者数と比べているので、「論文の感染者数と現実の感染者数を比較する誤り」に該当しています。

「論文は、推定感染者数が現実的な数値だという意味でその比較をしているのではない。ワクチンなしシナリオについての記述を読めば、シナリオが不自然で非現実的であることは分かるから、誤解する方がおかしい」との主張があるかも知れませんが、その主張は成立しません。

なぜならその誤解を避けるための論文の説明は明らかに不十分だからです。(6-5)節に示すように３つの学会の見解も「論文の感染者数と現実の感染者数を比較する誤り」に陥っています。専門家の集団である学会が誤解するほど、論文の説明は誤解しやすく分かりにくいのです。

Sci Rep 2023 論文のワクチンなしシナリオでの推定感染者数や死者数は、シナリオが不自然で非現実的であるとの分かりやすい説明が不十分な状態で示されています。この論文のこれらの記述は、少なくとも誤解の恐れが極めて大きいものであり、不適切です。

(6-2) 西浦氏の x.com への投稿における誤り

西浦氏は、2023-10-18 に Sci Rep 2023 論文についての投稿を x.com にしています。 https://x.com/nishiurah/status/1714629177385553981

京大と感染研の共同。反事実仮想を実効再生産数の成分で作成し、2021年予防接種2回が仮に無かった時の流行を作り因果推論を実施。2021年2月～11月末で6330万(6320-6360万）が感染し36.4万人が死亡する計算になり、実際には470万人感染・1万人死亡。差分は予防接種で逃れた。https://rdcu.be/doSNU

この投稿は、論文の推定感染者数を、現実の感染者数と比較しているので、「論文の感染者数と現実の感染者数を比較する誤り」に該当しています。

西浦氏は「反事実仮想を作成し」と述べていますが、これは論文の想定が不自然で非現実的であることを充分に説明していません。一方で西浦氏は「逃れた」と記述していて、これはあたかも「実際に感染を回避した人数を論文が示している」かのようです。

このような投稿は、誤解を招くものであり、不適切です。

なおこの投稿の記述には、論文の記述とやや不整合なところがあります [注6-2a]。

[注6-2a] 西浦氏の投稿の記述は、論文の「13.5倍」「36.4倍」とやや不整合なので、どちらかが誤っています。周辺の事情から考えると、「13.5倍」について誤っているのは論文の記述だと思われます。

(6-3) Sci Rep 2023 論文を紹介した産経の記事の誤り

産経は、2023-11-16 の記事「新型コロナワクチンで死者９割以上減　京都大推計」（同アーカイブ）で Sci Rep 2023 論文について報じました [注6-3a]。

この記事は、論文の推計結果だとして、ワクチンの接種によって研究期間中の感染者数と死者数を「いずれも９０％以上減らせた」と説明しています。この表現は論文の推定感染者数を、現実の感染者数と比較しているので、(3-5)節に示した「論文の感染者数と現実の感染者数を比較する誤り」に陥っています。よってこの記事は不適切です。

この記事には論文がどのような想定で計算されたかについての詳しい説明はありません。その結果、一般読者は示された感染者数や死者数を現実的な値と誤解し、ワクチンの効果を過大評価する恐れがあります。

このため、ワクチンの効果を過度に評価してしまう可能性があります。ワクチンは国民の健康に関する事項ですから、一般の読者に向けた記事は正確性において慎重であるべきです。この記事は慎重とは言えませんから、不適切です。

[注6-3a] 産経記事は共同通信からの配信によっていると思われ、ネット上には共同記事もありました。共同記事は現在はリンク切れです。アーカイブをご参照下さい。共同記事と産経記事の差はほとんどありません。

(6-4) 産経記事を紹介した西浦氏の投稿の問題

(6-3)節で不適切だと説明した産経記事を、西浦氏は x.com への投稿で「ぜひ多くの方に読んでいただきたい」と紹介しました。2023-11-16 の投稿 https://x.com/nishiurah/status/1725101388987019748 です。

共同通信からの配信です。ぜひ多くの方に読んでいただきたいニュースです「新型コロナワクチンで死者９割以上減　京都大推計」 https://sankei.com/article/20231116-3ICUWGMN3FMVZNSKJJGKPB4ARE/

西浦氏はこの投稿で、「新型コロナワクチンで死者９割以上減」との記事タイトルを拡散しました。しかし (6-3)節に述べたように、この記事には Sci Rep 2023 論文の不自然な想定の詳しい説明がなく、西浦氏の投稿にもその説明はありません。したがって西浦氏の投稿は不適切であり、一般読者が記事と同じ「論文の感染者数と現実の感染者数を比較する誤り」に陥る可能性や、ワクチンの効果を過大評価する可能性を招いています。またそれを「多くの方」に拡散しています。

(6-5) 日本感染症学会、日本呼吸器学会、日本ワクチン学会の見解の誤り

日本感染症学会、日本呼吸器学会、日本ワクチン学会（以下、三学会と略記します）は、2024-10-17 に「2024年度の新型コロナワクチン定期接種に関する見解」を発表しました。

このうち Sci Rep 2023 論文に関する付近を引用します。

わが国でも、新型コロナワクチンが導入されていなかったら、2021年2月から11月の期間の感染者数は報告数の13.5倍、死亡者数は36.4倍であったと推定されています ${ }^{2)}$ 。また、オミクロン株流行期の2022年1月から5月の東京都でも、直接的・間接的に感染者数を65%減少させたと報告されています ${ }^{3)}$ 。[注6-5a] [注6-5b]

引用部では、論文を参考文献に挙げながら「ワクチンがなければ感染者は報告数の13.5倍、死亡者数は36.4倍であった」との推定が示されています。これは、論文が推計した感染者数と現実の感染者数とを比較しているので、(3-5)節に示した「論文の感染者数と現実の感染者数を比較する誤り」に陥っています。

したがって見解のこの箇所は不適切です。見解の表現では、読者や政策決定者がワクチンの効果を過大評価してしまう恐れがあります。見解がこの論文の計算結果を用いるなら、誤解を避けるために、この論文が不自然で非現実的な想定で計算していることを明確にし、専門家の学会としての責任を果たす必要があります。

また、この見解には概要も示されています。見解の概要も、Sci Rep 2023 論文を示しながら「わが国でも2021年2～11月の死亡者数を大きく減少させたとされています」と述べていて、この記述は「論文の感染者数と現実の感染者数を比較する誤り」に陥っています。概要のこの箇所は不適切です。

この見解には西浦氏の別の論文 [Kayano 2023b] に関する問題もあります。この件については（１１）節で検討します。

[注6-5a] 引用中、"2)" で参照されているのは Sci Rep 2023 論文 [Kayano 2023a] です。"3)" で参照されているのは [Kayano 2023b] です。
[注6-5b] 見解の記述「13.5倍」「36.4倍」は、[注6-2a] に示した不整合に関するものです。三学会の見解は、(6-2)節の西浦氏の投稿と整合しています。論文、西浦氏の投稿、三学会の見解のうち、誤っているのは論文だと思われます。

（７）Sci Rep 2023 論文について述べた西浦氏の投稿の検討

西浦氏は、2023-11-01 の x.com に論文についてのスレッドを投稿しました。このスレッドの3つの投稿を順に検討します。

(7-1) 一つ目の投稿

一つ目の投稿はこちら（[url]、[アーカイブ]）です。

西浦氏は投稿で、

「実際には流行が大きくなったら人流が減って皆も接触を避けるから、ワクチンの成分だけを機械的に扱うのは反事実ではない。過大評価では？」→誤りです。ご指摘はもっともですが予防接種の「ある」「なし」の差分は予防接種のみを加味して計算すべきものです

などと述べています。

この投稿の、「誤りです」「ご指摘はもっとも」は何を指しているのか分かりにくいため、論旨を把握しにくいところがあります。以下ではこの点についての私の考えを示します。

西浦氏の投稿に（）で私の補足を追加し、論旨を把握しやすくしたものが以下です。

「実際には流行が大きくなったら人流が減って皆も接触を避けるから、ワクチンの成分だけを機械的に扱うのは（論文が計算するべき）反事実ではない。（論文の計算は）過大評価では？」→（計算したシナリオが論文が計算するべき反事実ではないとの指摘は）誤りです。（実際には流行が大きくなったら人流が減って皆も接触を避けるとの）ご指摘はもっともですが（論文が計算する）予防接種の「ある」「なし」の差分は（（４）節の説明のようにシナリオ作成に関する制約があるので）予防接種のみを加味して計算すべきものです

これなら西浦氏の投稿は（ある程度まで）論旨を把握できます。もう少し説明します。

投稿はまず、「ワクチンの成分だけを機械的に扱うのは反事実ではない」としています。反事実ならばどのようなシナリオを作っても構わないなら、直後に西浦氏が「誤りです」と否定しているのは腑に落ちません。しかし、（４）節に述べたように論文が作成できるシナリオに制約があることを考慮するとともに、「ワクチンの成分だけを機械的に扱うのは（論文が計算するべき）反事実ではない。」と補足すると、論旨を把握できるようになります。

補足したその部分は、（２）節で説明した意味において、「（論文が計算しているシナリオは不自然なので、）それは計算対象とすべき反事実シナリオではない」という質問者の主張を示しています。この主張に対して西浦氏は、（４）節の意味で「（シナリオは不自然かも知れないが、実質的に不自然なシナリオしか作成できないのだから、計算対象とすべきシナリオではないとの主張は）誤り」と述べているのです。

西浦氏が「実際には流行が大きくなったら人流が減って皆も接触を避ける」に「ご指摘はもっともですが」と答えているのは、（２）節で説明した通り、それが本来の人々の自然な行動だからです。その後の「予防接種の「ある」「なし」の差分は予防接種のみを加味して計算すべきものです」は、（４）節で説明した「シナリオの制約があるために、（ワクチンなしシナリオは）予防接種のみを加味して計算するしかない」との事情を述べているのです。

これで西浦氏の投稿の意味が分かるようになってきました。

ただし、このように（（２）節や（４）節での検討を踏まえて）多くを補足しなければ論旨を把握しにくい西浦氏の投稿は適切とは言えません。特に、「誤りです」と「ご指摘はもっともですが」が何を指しているのか曖昧なので論旨を把握しにくくなっています。

本節で示した補足は私の考えです。西浦氏の投稿をより一貫して把握できる他の補足があるならば、伺いたいと思います。よろしくお願いします。

(7-2) 二つ目の投稿

二つ目の投稿はこちら（[url]、[アーカイブ]）です。

「6千万人くらい人口の約半分が感染した場合は重症患者が収容しきれない。入院できないと患者を助けられなくなって致死率が高くなる。過小評価では？」→　誤りです。現実的に致死率が高くなる影響は医療提供体制の限界によって起こるもので、予防接種の「ある」「なし」の因果推論とは無関係

との投稿を検討すると、西浦氏がこの論文の計算値を「現実的」なものだと考えていないことが分かります。

西浦氏は「人口の約半分が感染した場合は重症患者が収容しきれない。入院できないと患者を助けられなくなって致死率が高くなる。」との懸念に対し、「現実的に致死率が高くなる」ことを認めています。

西浦氏はこの論文の計算に、「（感染が大幅に拡大した時に）現実的に致死率が高くなる」という効果を算入していません。投稿の西浦氏はこの効果を計算で考慮しなくていいと述べていますし、論文の致死率はシナリオによって変化しないからです [注7-2a]。西浦氏に、この論文で「現実的」な死者数を計算しようという意図はないのです。したがってこの論文の感染者数も現実的な計算値は意図していません。（各年齢層で死者数と感染者数は比例するからです。）

西浦氏は、本稿が指摘する「論文の感染者数と現実の感染者数を比較する誤り」を、別の形で確認したことになります。

なお、この論文が現実的な値の死者数や感染者数の計算を意図していないなら、西浦氏はそのことを論文の限界事項（limitations）に書くべきでした。また、医療提供体制の限界を考慮しないなら、西浦氏はこの点も limitations に書くべきでした。これらは x.com にではなく、論文に書くべきことです。

[注7-2a] 論文式(12) や、補足情報（41598_2023_44942_MOESM1_ESM.docx）の Supplementary Figure S11 にあるように、感染者死亡率 $\lambda_a$ は、感染者報告率と年齢層で変化しますが、シナリオでは変化しません。

(7-3) 三つ目の投稿

三つ目の投稿はこちら（[url]、[アーカイブ]）です。

これらは単なる知的体操の問題なんですが、要するに「他の条件が全部一緒だとして、予防接種だけなかった場合に」というのを非現実的だとしても仮想的に作っているということですよね。そのような仮想に加えて、現実にあわせた仮想も政策判断では重要になりそうですが。

この投稿は、本稿の論旨と比較的整合性が高いです。

西浦氏の投稿は、まず一つ目の投稿や二つ目の投稿を指して（したがって論文についての疑問を指して）、

これらは単なる知的体操の問題なんですが、

としています。西浦氏は単に「知的体操」と述べていますが、これはより分かりやすく「専門家間における知的体操」と書くべきでした。これは誤解されやすい特殊な論文であり、専門家間でのみ議論されるべきものと言えるからです。この三つ目の投稿は、この点の説明を意図したのかも知れませんが、投稿の表現だとこの意味はほとんど伝わりません。西浦氏は「知的体操」と書いた含意を、より明確にすべきでした。専門家である西浦氏と同様の知的体操を、一般の人が行う必要はないからです。

投稿はその後、論文のシナリオについて以下のように述べています。

要するに「他の条件が全部一緒だとして、予防接種だけなかった場合に」というのを非現実的だとしても仮想的に作っている

西浦氏はここで、論文が仮想的に作ったシナリオが「非現実的だ」と、述べています。これは本稿が（２）節の「雨と傘の例え」などで説明した内容であり、この論文の最も重要な性質を示しています。西浦氏はこの点を論文でより丁寧に説明すべきでした。

また西浦氏はここで、論文のシナリオを「他の条件が全部一緒だとして、予防接種だけなかった場合に」と表現しています。これは、(5-2)節に説明した論文式(3) そのものです。当たり前のことですが、西浦氏の投稿は、論文の数式と整合しています。

投稿はその後、

そのような仮想に加えて、現実にあわせた仮想も政策判断では重要になりそうですが。

と述べています。ここでも西浦氏は、論文の仮想シナリオが「現実にあわせた」ものではない（論文の仮想シナリオは非現実的なものだ）と、本稿（２）節が示した内容を実質的に繰り返しています。ただし西浦氏は、現状の Sci Rep 2023 論文も政策判断で重要であるかのように書いていますが、この論文の計算結果は（専門の学会ですら誤解するほど）極めて誤解されやすいものです。この論文を政策判断に用いるのは、誤解を招かないようにしてからにするべきです。

（８）Sci Rep 2023 論文の意義の再検討

そもそも本稿は、全体として Sci Rep 2023 論文の意義を検討していますが、本節では特に、他であまり検討してこなかった二つの事項について述べます。

(8-1) Sci Rep 2023 論文の計算結果が政策判断の助けになるかは疑問

一般に、ある論文が何らかの値を推定した場合、その値が正確でなくても、政策判断の助けになることはあります。しかし Sci Rep 2023 論文はそうした論文に該当しないと思われます。

この論文の推定値が政策判断の助けになるには、その推定値がどの程度信頼できるのかについての情報が少なくとも必要です。論文は、Figure 1 などで 95% 信頼区間を示しているので、これを示しているようにも見えます。

しかしこの論文のように「全て」がモデルに基づく計算での信頼区間は、そもそも信頼区間計算の妥当性が自明ではなく、不適切な信頼区間を計算することさえ可能です。したがって西浦氏は、信頼区間の正当性を示すためには、信頼区間計算の詳細を開示する必要があります。しかし論文はこれを開示していません。だから論文に書かれている信頼区間の信頼性は、不明です。

またそもそも、行動変化と実効再生産数との関係が不明であることを示した（４）節の検討を踏まえると、この論文の感染者数の推定値がどの程度過大なのかは、論文著者にも不明です。どの程度過大なのか不明な推定値についての信頼区間は、仮に計算されたとしても信頼できる数値にはなりません。またどの程度過大なのかが不明な推定値が政策判断の助けになるかが疑問であることは、ご説明するまでもありません。

さらに (4-1)節で検討したように、Sci Rep 2023 論文には現実社会をモデル化しようとの意図が最初からなかったと考えられますし、(7-2)節で検討したように、西浦氏は投稿でも現実的な計算の意図を実質的に否定しています。

このような論文の推定値を政策判断に使うことは、妥当ではありません。

(8-2) 一般の人にとって Sci Rep 2023 論文とは

Sci Rep 2023 論文のような計算を専門家が行い、それを論文として報告することは、仮に論文の内容に問題があったとしても一定の意味があるのかも知れません。

しかしこの論文は、想定が不自然で非現実的な論文・計算であり、過大な感染者数を計算している上にそれが明示されていません。これは一般の人が内容を見聞して理解することが要請されたり、奨励されたりするような論文ではありません。論文が推定値の過大さを明示していないので、一般の人はその結果を現実の感染者数と比較してしまう恐れがあります。

およそ論文というのは専門的なのですが、この論文はとりわけ特殊で専門性の高い論文です。したがって一般の人がこの論文に注目する必要はなく、この論文は「専門家間の知的体操」だと考えるのが適切です。

（９）論文への誤解の原因と西浦氏の責任

(9-1) Sci Rep 2023 論文の説明不足と、それによる誤解の拡散

Sci Rep 2023 論文についての誤り（「論文の感染者数と現実の感染者数を比較する誤り」）が広がった背景には、主に四つの要因があります。

一つ目は、論文が採用している論理が誤解されやすいことです。専門家がその専門分野における被害想定を計算する際、（実現しないことがはっきりと分かっている）非現実的な想定で計算することはほとんどありません。（論文がこのような特殊な計算をした理由が理論的な限界のためであることは、（４）節で説明しました。）

二つ目は、論文が誤解されやすいポイントを分かりやすく説明していないことです。西浦氏にとって、この論文が誤解されやすいことは、意外ではないはずです。本稿が指摘しているこの論文についての誤り（「論文の感染者数と現実の感染者数を比較する誤り」）は、このような論理構成の論文では予想される誤りです。したがって西浦氏は、この論文が誤解されないよう、充分に注意を払うべきでした。論文がこの点を明確にしていれば、誤解を防ぐ余地はあったはずです。

三つ目は、論文自体ではなく西浦氏による x.com への投稿の問題です。西浦氏の投稿は、本節の一つ目、二つ目の問題による論文の誤解を正すのではなく、むしろ誤解を招いています。論文の誤解されやすさを最もよく知る西浦氏による不適切な投稿ですから、その責任は大きいです。

四つ目は、論文に関して述べられるその他の言説です。産経記事が誤り、約一年後には専門家の集団である三学会も誤りを含む見解を出しています。

このように拡散された誤解は、ワクチンへの「優良誤認」を引き起こし、ワクチンへの過剰な期待や誤った判断に基づくワクチン接種を招く可能性があります。また、専門家や専門家集団の説明責任が果たされていないことは、政策決定者や一般市民に不信感を与える可能性があります。

(9-2) 西浦氏が説明すべきこと

論文の著者である西浦氏は、Sci Rep 2023 論文の非現実的な想定やその計算結果の考え方について、明確で丁寧な説明を行い、日本社会に広がっている誤解を解消する責任があるのではないでしょうか。

具体的には、

ワクチンなしシナリオが不自然で非現実的な想定のシナリオであること。（２）節。
論文が計算する感染者数や死者数が、現実的な値を意図したものではないこと。(4-1)節、(7-2)節。
論文が計算する感染者数や死者数が、過大な値だと分かっていること。(2-2)節。
論文が計算する感染者数と現実の感染者数を比較してワクチンの効果だと述べてはいけないこと。(3-5)節。
論文を根拠とした不適切な記述のある産経記事は修正すべきであること。(6-3)節。
論文を根拠とした不適切な記述のある三学会の見解は修正すべきであること。(6-5)節。
論文が政策判断の助けになるかは疑問であること。(8-1)節。

を改めて説明すべきです。

（１０）政府や企業の対策に関するシナリオの問題点

ここで述べるのは、「雨と傘の例え」では煩雑になるので省略した事項です。

Sci Rep 2023 論文の考え方では、ワクチンなしシナリオでの政府や企業などの対策は、現実と同じ時に同じ対策を実施すると考えます。例えばワクチンなしシナリオで緊急事態宣言を開始した日、終了した日は、現実で宣言を開始した日、終了した日と同じです。ワクチンなしシナリオでどんなに感染が拡大しても、現実と同じ日より早く宣言を開始することはありません。また感染の拡大状況に関わらず、現実と同じ日には宣言を終了します。この点を「雨と傘の例え」では省略しましたが、これを含めて検討してもますますワクチンなしシナリオが不自然になるだけなので、省略したことによる本稿の論旨への影響はありません。

（１１）[Kayano 2023b] における、Sci Rep 2023 論文と同じ構造の問題

西浦氏は、2023-10 に複数の論文を発表しました。本稿で検討してきた、全国での感染者数などを論じた Sci Rep 2023 論文 [Kayano 2023a] と、東京での感染者数などを論じた別の論文 [Kayano 2023b] です [注6-5b]。 [Kayano 2023b] も仮想シナリオを構築し、そこにおけるワクチン接種率を仮想的に変更してワクチンなしシナリオを作成し、そこでの感染者数を推定しています。

[Kayano 2023b] のシナリオには、Sci Rep 2023 論文のシナリオと同じ問題があります。「ワクチンなしになったことで感染者数が増大しているのに、人々の行動などが変化しない」との不自然で非現実的なシナリオだという問題です。したがって [Kayano 2023b] の推定値を、現実の感染者数と比較することも不適切です。ところが (6-5)節で述べた三学会の見解は、この論文にも言及していて、関係する部分は

また、オミクロン株流行期の2022年1月から5月の東京都でも、直接的・間接的に感染者数を65%減少させたと報告されています ${ }^{3)}$ 。

となっています。"3)" が [Kayano 2023b] を参照しています。この引用部は、この論文の推定感染者数を現実の感染者数と比較しているので、(3-5)節に示した「論文の感染者数と現実の感染者数を比較する誤り」に陥っています。

したがって三学会の見解のこの部分も不適切です。

（１２）結論

本稿は、Sci Rep 2023 論文が想定する『ワクチンなしシナリオ』が不自然で非現実的であることを指摘し、その計算結果が現実の感染者数や死者数と比較されることの問題点を明確にしました。

論文のワクチンなしシナリオがどれほど現実的でないかを、「雨と傘の例え」で説明しました。小雨で傘を差していた人が、大雨で傘がなくても同じ行動をするなどのシナリオは、感染拡大に伴う行動の変化を無視しています。これは不自然であり非現実的です。

その結果この論文が計算する感染者数は過大になっています。論文の計算結果を現実的なものとして扱うべきではなく、論文の計算結果に言及する場合には、この想定の特殊性を踏まえる必要があります。

Sci Rep 2023 論文の計算結果を扱う場合によくみられる誤解として、「論文の感染者数と現実の感染者数を比較する誤り」を示しました。論文の「ワクチンなし」の推計感染者数を現実の推計感染者数と比較し、それをワクチンの効果とするのは不適切です。

産経記事や三学会（日本感染症学会、日本呼吸器学会、日本ワクチン学会）の見解は、この論文の特殊な想定を説明せずにその計算結果を現実の感染者数と比較し、ワクチンの効果としています。したがって「論文の感染者数と現実の感染者数を比較する誤り」に陥っています。これにより、読者や政策決定者がワクチンの効果を過大評価する可能性があります。

この論文は、「ぜひ多くの方に読んでいただきたいニュースです」などと一般読者に向けて推奨されるような論文ではありません。この論文が扱うシナリオは不自然で非現実的な想定に基づいているからです。計算結果を紹介する際には、その特殊性を充分に説明し、誤解を避ける責任があります。

Sci Rep 2023 論文の誤解がこれ以上拡散することを防ぐには、論文著者である西浦氏や学会が、論文の想定や計算の結果の限界について積極的に説明する必要があります。そして、政策決定者や社会に誤った印象を与えないよう努めるべきです。

（参考文献）

（付録）

(付録Ａ) 本稿に関係のある url など

本稿に言及している x.com のスレッド [url]（まだ書いてません。）

(付録Ｂ) 本稿に出てくる url とアーカイブ

参考文献以外の url とアーカイブのリスト。本文中に示したものもあります。

2023-10-18 西浦氏の x.com への投稿。Sci Rep 2023 論文を紹介したもの。[url] [アーカイブ]
2023-11-01 西浦氏の x.com への投稿。「FAQにお答えしましょう」「非現実的」「知的体操」を含む3つの投稿によるスレッド。[url] [アーカイブ]、[url] [アーカイブ]、[url] [アーカイブ]
2023-11-16 産経記事「新型コロナワクチンで死者９割以上減　京都大推計」 [url] [アーカイブ]
2023-11-16 共同記事「コロナワクチンで死者9割以上減　京都大チームが推計」 [url] [アーカイブ]
2023-11-16 西浦氏の x.com への投稿。「ぜひ多くの方に読んでいただきたい」など [url] [アーカイブ]
2024-10-17 日本感染症学会、日本呼吸器学会、日本ワクチン学会「2024年度の新型コロナワクチン定期接種に関する見解」 [url] [アーカイブ]
2024-10-17 日本感染症学会、日本呼吸器学会、日本ワクチン学会「2024年度の新型コロナワクチン定期接種に関する見解（概要版）」 [url] [アーカイブ]
2024-10-21 上2件へのリンクがある日本感染症学会のお知らせ [url] [アーカイブ]
幾つかの図版は [url] 以下を参照しています。

（更新履歴）
2024-12-17
公開。
2024-12-20
(6-5)節に、「西浦氏の別の論文 [注6-5b]」と書いていましたが、「西浦氏の別の論文 [Kayano 2023b]」が正しい表現だったので修正しました。
2024-12-21
以下の修正を行いました。これらによる論旨の変更はありません。
- (2-1)節の「反事実シナリオ」との表記を「反事実仮想シナリオ」に修正しました。
- (2-1)節の末尾に、「またこの例えは、」から「済んでいます」までを追記しました。
- (2-4)節を追加しました。
2024-12-22
[Nakamura 2024a]、[Nakamura 2024b] を参考文献に加え、これらの紹介を（１）節に加えました。
2024-12-25
以下の修正を行いました。これらによる論旨の変更はありません。
- (2-5)節を追加しました。
- (2-4)節の見出しを、(2-5)節との対比を考慮して変更しました。
2025-01-16
以下の修正を行いました。これらによる論旨の変更はありません。
- (2-5)節に論文式(3) を加筆し、関連する説明を追加しました。
- [Kayano 2023a] の著者名の表記を改めました。
2025-01-22
counterfactual の訳語として、反事実仮想を使っていましたが、引用の部分を除いて反実仮想に改めました。これによる論旨の変更はありません。
2025-02-11
x.com 投稿を引用する際の形を整えました。これによる論旨の変更はありません。
2025-11-26
(7-1)節に少し加筆しました。論旨の変更はありません。

2024-06-21

ネット上でしていることのまとめ

「接触8割減」の問題をまとめた論考はこちらに。
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

ネット上でしていることのまとめです。
今のところ全部、コロナ関連です。

(1) 主な発言のリスト
- (1-1) 新型コロナ関連の主な事柄のリスト（特に重要な項目）（2022-01-30 更新）
- (1-2) 新型コロナ関連の主な事柄のリスト（2022-04-25 更新）
(2) 比較的詳しく検討したこと（検討事項別）
(3) （インストール不要で）SIR モデルを計算できるスクリプト
(4) SIR モデルを計算できるスプレッドシート
修正履歴

(1) 主な発言のリスト

主な発言のリストです。

「主な発言」と言いつつ、沢山あります。
(1-1)の「特に重要な項目」の中には、(2)の「最初の緊急事態宣言「接触8割減」の根拠への疑問」も幾つか含まれています。

(1-1) 新型コロナ関連の主な事柄のリスト（特に重要な項目）（2022-01-30 更新）

新型コロナ関連の主な事柄のリスト（特に重要な項目）です。

https://sarkov28.hatenablog.com/entry/2021/01/25/193753

(1-2) 新型コロナ関連の主な事柄のリスト（2022-04-25 更新）

新型コロナ関連の主な事柄のリストです。

https://sarkov28.hatenablog.com/entry/2021/01/25/193020

(2) 比較的詳しく検討したこと（検討事項別）

比較的詳しく検討した事項です。
話が長くなってしまうのは私の力不足もあると思いますが、不足する情報を議論で補う必要があるからでもあります。

(2-1) 「接触8割減」に関して

「接触8割減」は重要な論点なので、多くを書いています。

先に書いていたのは (2-1-3) の一連であり、後に書いたのが (2-1-1) と (2-1-2) の一連です。
(2-1-1)(2-1-2) はいずれ (2-1-3) の一部に組み込む予定です。
(2-1-4)(2-1-5) は、「接触8割減」の関連ですが、別の問題を書いています。

(2-1-3) では、「傾いた水平線」などグラフの問題の他、首相の国会答弁に関する事項や、緊急事態宣言に同意した諮問委員会での奇妙な議論についても検討しています。

(2-1-1) で主に検討しているのは、(2-1-3) では触れていない、根拠のグラフの理論的な問題（ややこしいが破壊的な問題）です。

(2-1-1) 「接触8割減」政策の科学的根拠

「接触8割減」に関する事項をまとめた論考
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

(2-1-2) (2-1-1) の論考に関連する事項

西浦氏ら専門家が示すべきだった「接触8割減」の説明
https://sarkov28.hatenablog.com/entry/2024/06/17/150500
西浦氏は「接触8割減」の数理モデルを示していない
https://twitter.com/sarkov28/status/1803703457955844230
「2020年春の西浦氏の言動は概ね妥当だった」と考えている方々に、確認したいことがあります。
西浦氏は、「接触8割減」の数理モデルを示していません。これは明確に不適切です。 https://sarkov28.hatenablog.com/entry/2024/06/19/213400
https://twitter.com/sarkov28/status/1803730841371345170

(2-1-3) 最初の緊急事態宣言「接触8割減」の根拠への疑問

[最初の緊急事態宣言「接触8割減」の根拠への疑問] として、複数のスレを書いています。
このスレ群は、まだ途中です。

twitter における目次 https://twitter.com/sarkov28/status/1463852276494180352
blog における目次 https://sarkov28.hatenablog.com/entry/2021/11/25/214039

twitter の目次の方が、図が入っているのでやや見やすいです。

この一連の問題で中心となるグラフ。2020-04-22 専門家会議の資料から。
このグラフについてはスレ [その1] などで説明してます。

グラフを根拠とした首相の国会答弁。グラフの誤りが答弁の誤りにつながっています。
グラフと答弁との繋がりについてはスレ [その4] などで説明しています。

首相の国会答弁が、接触削減の効果を不適切に述べていたことを視覚化しています。
このグラフについてはスレ [その4] などで説明しています。

(2-1-4) 「接触8割減」の根拠は意図的に間違って説明されたのでは

私は、
西浦氏が、自身への批判を一時的に逸らすために、「「接触8割減」の根拠」について、BuzzFeed 記事で意図的に間違った説明をしたのではないか、
と疑っています。
この件について書きました。

目次
https://twitter.com/sarkov28/status/1607700401067024385
(a)「2020-04-07 の tweet 動画で西浦氏が示した「接触8割減」の根拠」は大雑把であり、説得力に乏しいものだった。
https://twitter.com/sarkov28/status/1607702103178506240
(b)「2020-04-11 掲出の BuzzFeed 記事での説明」は、「接触8割減」の根拠が確かなものであるかのような印象を与えた。
https://twitter.com/sarkov28/status/1607706185117110273
(c) ところが、2020-12 刊行の西浦氏共著書によると、BuzzFeed 記事の説明(b)は「接触8割減」の根拠ではなかった。説明(b)は、間違っていた。
https://twitter.com/sarkov28/status/1607711194571501568
(d) 説明(b)のために、西浦氏の説明(a)に対して「大雑把だ」と批判しにくくなっている。西浦氏は、間違った説明(b)を意図的に行った疑いがある。
https://twitter.com/sarkov28/status/1607714002368606208

(2-1-5) 「西浦氏は「傾いた水平線」を意図的に描いた」と考えられる

（2024-06-20 の注記：本項の内容には詰めが甘いところがあると考えています。修正する可能性があります。）

西浦氏は「傾いた水平線」を少なくとも2回、グラフに描いていることが分かりました。
これは科学を踏みにじる行為です。
2回もこんなことをするのは、意図的な行為だと考えるのが自然です。

まだ書き終えておらず未整理ですが、以下のスレがその一部になります。

「西浦氏は「傾いた水平線」を意図的にグラフに描いた」と考えられます。
西浦氏が「傾いた水平線」を少なくとも2回、グラフに描いているからです。
2回もこんなことをするのは、意図的な行為と考えるのが自然です。
https://twitter.com/sarkov28/status/1668175347895136257
特にこのスレにおける fig.6、fig.7 が重要です。
西浦氏は、「傾いた水平線」のグラフを少なくとも4枚示しています。
https://twitter.com/sarkov28/status/1668499871899471872

(2-2) 人流削減と接触削減の関係に関する混乱

西浦氏には、「接触8割減のために必要な人流削減は、どれだけか」という基本的な論点での混乱がありました。 2020-04-07 に緊急事態宣言を発出した時点の西浦氏には、「接触8割減のために必要な人流削減は、どれだけか」についての定まった考えが無かったとしか思えません。

[接触削減の評価方法（人流削減から接触削減を計算する方法）の大混乱] として書いたのはこの件です。

(2-2-1) 概要にはこの件の概要を書きました。(2-2-2) 詳細には、この件を詳しく書きました。

(2-2-1) 接触削減の評価方法の大混乱概要

「接触8割減のために必要な人流削減は、どれだけか」
これは接触削減における基本的な質問です。西浦氏には、最初の緊急事態宣言を発出した 2020-04-07 の時点で、この件の定まった考えが「ありませんでした」。市民に「接触削減を」と呼びかけていた西浦氏に、この件の定見がなかったというのは、控え目に言っても極めて不適切です。
https://twitter.com/sarkov28/status/1787063999638741474

(2-2-2) 接触削減の評価方法の大混乱詳細

［接触削減の評価方法の大混乱］として、複数のスレを書きました。
この件は、西浦氏が意図してやったことなのが明らかだという特徴があります。
また、一連の検討によって、「接触8割減」を提唱した 2020年4月の初めの時点で西浦氏の理論疫学に重要なものが欠けていたことが明らかになりました。それについては［その7 まとめ西浦氏の理論疫学に欠けていたもの］で書きました。

概要
https://twitter.com/sarkov28/status/1787063999638741474
目次
https://twitter.com/sarkov28/status/1581947544984133634
［その1 戦術と西浦氏の意図］
https://twitter.com/sarkov28/status/1581927071370002432
［その2 戦術1］
https://twitter.com/sarkov28/status/1581961107635245057
［その3 評価方法の変遷と必要な人流削減量］
https://twitter.com/sarkov28/status/1584474885891710976
［その3］に関連して書いたブログ接触8割減」に必要な人流削減は、ほぼ55％
https://sarkov28.hatenablog.com/entry/2022/10/21/233456
［その4 戦術2～3］
https://twitter.com/sarkov28/status/1584540933680660482
［その5 接触頻度の3つの使用法］
https://twitter.com/sarkov28/status/1587414490303279104
［その6 戦術4～5］
https://twitter.com/sarkov28/status/1587727801976647680
［その7 まとめ西浦氏の理論疫学に欠けていたもの］
https://twitter.com/sarkov28/status/1600833369927208960
接触削減の評価方法の大混乱 [資料]
https://sarkov28.hatenablog.com/entry/2022/10/21/225701

(2-3) 「42万死亡推計」に関して

「42万死亡推計」に関しても、多くを書いています。

(2-3-1) 発表の後に適切な補足がなかったこと

「何も（感染症対策を）しなければ」に関して
https://twitter.com/sarkov28/status/1720605623266480476
基本再生産数の値がわかっていなかったこと関して
https://twitter.com/sarkov28/status/1759201640668893184

(2-3-2) 西浦氏は「「42万死亡推計」は実現しない」と考えていた

西浦氏が「「42万死亡推計」は実現しない」と発表時点で考えていたことを示す2つの根拠
https://twitter.com/sarkov28/status/1721828648804897138
「「42万死亡推計」は 2020-04-27 時点の知見で間違っていた」との西浦氏による説明
https://twitter.com/sarkov28/status/1758669701163651393

(2-3-3) 西浦氏が github で開示しているパラメータの誤り

西浦氏が github で開示している「42万死亡推計」のパラメータの一部に2％ほどの誤りがある
https://sarkov28.hatenablog.com/entry/2024/03/16/092400
この誤りのために、計算結果は「42万」と2％ほど異なる値になります。
私は適切だと思われるパラメータを示しています。
西浦氏が示す「42万死亡推計」のパラメータの不自然さ
https://sarkov28.hatenablog.com/entry/2024/03/17/061200
これは、「西浦氏のパラメータに2％ほどの誤りがある」との別稿の傍証になっています。「2％ほどの誤りがある」との指摘は、直接の根拠であるプログラムを開示していますので傍証は不要なのですが、プログラムの参照を要さない不自然さがあるのでご説明するものです。

(2-3-4) 「42万死亡推計」の問題点に連なる事項

「42万死亡推計」は、2020-03-19 専門家会議の資料と同じ計算
https://sarkov28.hatenablog.com/entry/2024/03/22/152040
これは「42万死亡推計」の性質を理解する上での重要事項なので示しています。
「42万死亡推計」の計算方法では、「死亡者数」は「感染者総数」にほぼ比例する
https://sarkov28.hatenablog.com/entry/2024/03/07/213500
これは意外なことではありませんが、重要な事項なのでご説明しています。

この件は、現時点（2024-03-25）で他にも準備中です。

(2-4) 東洋経済の実効再生産数の簡易計算に関する諸問題

東洋経済の実効再生産数の簡易計算は、西浦氏の監修によるものです。
コロナ騒動では、この計算が各所で参照されていました。

以下で私が示すのは、「東洋経済の実効再生産数の簡易計算式は、通常言われている実効再生産数とは異なる値を計算する」ということです。
これは「異なる値の疑い」ではなく、「異なる値」であることがはっきりしています。
[1.概要]、[2.東洋経済の計算式はどこが間違っているのか] をご参照下さい。

特に、感染拡大初期においては、
「東洋経済の実効再生産数の簡易計算式」を toyoRt 、「通常言われている実効再生産数」を sRt とした時、この両者の間には、
$toyoRt = e^{sRt - 1}$
という関係式が成立します。
この関係式については、[1.概要] で説明し、[6. 東洋経済の計算式と、通常言われている実効再生産数との関係式の導出] で導出を示しています。

[0.目次]
https://twitter.com/sarkov28/status/1405140064561029120
[1.概要]
https://twitter.com/sarkov28/status/1402934465261756416
[2.東洋経済の計算式はどこが間違っているのか]
https://twitter.com/sarkov28/status/1405099777688170498
[3.西浦氏による例示その1(東洋経済の計算式で不適切になる例その1)]
https://twitter.com/sarkov28/status/1437747938713686025
[4.西浦氏による例示その2(東洋経済の計算式で不適切になる例その2)]
https://twitter.com/sarkov28/status/1440880535002234890
[5.西浦氏による例示その3(東洋経済の計算式を使っている例)]
https://twitter.com/sarkov28/status/1440972220856078341
[6.東洋経済の計算式と、通常言われている実効再生産数との関係式の導出]
- twitter での説明はまだです。
  （数式を多用するので、twitter での説明は概略になりそうです。）
- ブログでの説明。
  https://sarkov28.hatenablog.com/entry/2023/07/19/140000
[7.上記関係式に関する追加の考察]、の予定
[8.まとめっぽいこと]、の予定

(2-5) 反実仮想シナリオ論文（Sci Rep 2023-10）の問題点

この論文については複数のブログ記事を書きました。

2025-04-19（論文執筆から 1年半ほど後）に西浦氏は、zenodo に関連情報を開示しました。書いた記事の一部は、この情報開示を受けた修正（補足）をすべき状態です。

以下に挙げるのは、

情報開示の影響を受けない記事、
必要な修正を済ませた記事、
この情報開示の問題を指摘した記事

です。

西浦氏の Scientific Reports 論文について（１）
論文の最大の特徴は、類のない非現実的な想定
https://sarkov28.hatenablog.com/entry/2023/12/27/215500
西浦氏の Scientific Reports 論文について（３）
活動度は報告率によって変化すべきではない
https://sarkov28.hatenablog.com/entry/2023/12/30/171500
西浦氏の Scientific Reports 論文について（７）
「ワクチンで感染者が９割減」は誤り
https://sarkov28.hatenablog.com/entry/2024/12/17/184600
西浦氏の Scientific Reports 論文について（８）
論文が採用しているワクチン効果への疑問
https://sarkov28.hatenablog.com/entry/2025/02/19/234000
西浦氏の Scientific Reports 論文について（１０）
論文 Figure S5 の妥当性への疑問
https://sarkov28.hatenablog.com/entry/2025/03/28/172800
西浦氏の Scientific Reports 論文について（１１）
開示されたプログラムの問題点
https://sarkov28.hatenablog.com/entry/2025/05/27/163000

(3) （インストール不要で）SIR モデルを計算できるスクリプト

（インストール不要で）SIR モデルを計算できるスクリプトを公開しています。

gmail のアカウントがあれば、
特になにもインストールなどをしなくても、
SIR モデルを計算して、
グラフを描けるスクリプト

をこちら
https://sarkov28.hatenablog.com/entry/2022/04/01/201503
で公開しています。

計算やグラフ表示はブラウザ上で行います。
実行するのは簡単です。私が作成したスクリプトのパラメータを変えて実行することもできます。

スクリプトで行っているのは、

「42万死亡推計」の再現、
西浦氏の「42万死亡推計」の情報開示のパラメータが不適切であることの説明、
西浦氏が「42万死亡推計」を説明した Newsweek グラフの再現、

などです。

(4) SIR モデルを計算できるスプレッドシート

SIR モデルを計算できるスプレッドシートを公開しています。

SIR モデルを計算して、
西浦氏のグラフを再現している、
スプレッドシート

をこちら
https://sarkov28.hatenablog.com/entry/2023/02/27/090000
で公開しています。

「42万死亡推計」も再現しています。
計算やグラフ表示はブラウザ上で行います。
四則演算しか使っていません。
python を使った、より精度がいいと思われる方法と計算結果を比較し、スプレッドシートでの計算結果が割と良い精度で西浦氏の計算を再現していることを確認しています。

修正履歴

2022-03-29
公開
2023-02-27
「SIR モデルを計算できるスプレッドシート」の件を追加しました。
2023-06-17
(2) を作成し、(2-1)～(2-3) を、(2) の下に移動しました。
この下に入る項目が増えそうだからです。
(2-4) を作成しました。
2023-07-29
(2-5) を作成しました。
2024-03-18
(2-6) を作成しました。
2024-03-25
(2-6) に項目を追加しました。
2024-06-06
(2-3) を (2-3-2) に移動し、新たに (2-3-1) を作成しました。
2024-06-20
(2) を大幅に組み替えました。
2025-06-13
- (2-2-2) に「概要」を追加しました。
- (2-5) を作成しました。

2024-06-19

西浦氏は「接触8割減」の数理モデルを示していない

「接触8割減」の問題をまとめた論考はこちらに。
https://sarkov28.hatenablog.com/entry/2024/05/17/213470

私がネット上でしていることのまとめは、こちらに。
https://sarkov28.hatenablog.com/entry/2022/03/29/160915

「2020年春の西浦氏の言動には小さな問題はあったかも知れないが、概ね妥当だった」と考えている人は今でもいると思います。その方々に私は確認したいことがあります。

西浦氏は、「接触8割減」の数理モデルを示していません。これは明確に不適切ですよね。これは小さな問題ではありません。「概ね妥当」な西浦氏なら、国民に説明すべき重要事項は全て説明しているはずです。

少なくともこの件があるので、2020年春の西浦氏を「概ね妥当だった」とすることはできないのではありませんか。

（１）序論：この問題での西浦氏の不適切さは明確
（２）なぜ数理モデルが必要なのか
（３）数理モデルが示されなくてもいいと考えるのは危険
（４）「接触8割減」の数理モデルは示されていない
（５）結論
更新履歴

（１）序論：この問題での西浦氏の不適切さは明確

「接触8割減」の数理モデルというのは、2020-04-22 専門家会議の「提言」の図2 を描くのに使われた数理モデルです。

2020-04-22 専門家会議「提言」図2

西浦氏に批判的な方には、「「接触8割減」の数理モデル不提示」という論点は地味に見えるかも知れません。問題視すべきもっと大きな問題が他にあるではないか、と。

もちろん私は、当時の西浦氏には大きな問題が他にも多数あったと思っています。しかし「「接触8割減」の数理モデル不提示」は、

数理モデルが示される必要があるのが明確で、
数理モデルが示されていないことが明確である、

という問題なので、事実関係がはっきりしています。これがこの問題の特徴の一つ目です。

また、問題の中核が「数理モデルが示されているか／示されていないか」というシンプルな話であることが特徴の二つ目です。例えば、私が別に指摘している「接触8割減」のグラフが科学的に間違っているという問題と比べて、話が簡潔なのです。

これらの特徴により、この件に関する西浦氏の不適切さは、明確で簡潔です。以下の（２）では数理モデルが示される必要があることを示します。（３）では同じ主旨を別の角度から示します。（４）では数理モデルが示されていないことを示します。（５）では結論を述べます。

（２）なぜ数理モデルが必要なのか

「接触8割減」の数理モデルが示される必要があるのは、この数理モデルが、国民全体の自由と権利を侵害する「接触8割減」政策の根拠だからです。こうした政策の根拠は明示されている必要があります。

緊急事態宣言は、新型インフルエンザ等対策特別措置法の第３２条を根拠として発出されました。この法律の第５条には、

国民の自由と権利が尊重されるべきことに鑑み、新型インフルエンザ等対策を実施する場合において、国民の自由と権利に制限が加えられるときであっても、その制限は当該新型インフルエンザ等対策を実施するため必要最小限のものでなければならない。

とあります。「接触8割減」政策が必要最小限かどうかを判断するには、数理モデルが必要です。このことからも、「接触8割減」の数理モデルは開示される必要があります。

（３）数理モデルが示されなくてもいいと考えるのは危険

（２）の説明があっても、この数理モデルを示す必要はないと思う方はいるでしょうか。

一般にグラフは、何らかの方法で測定したデータから描画します。市中で測定したり、実験室内で測定したりします。測定の信頼性が、グラフの信頼性を左右します。

数理モデルからグラフを描く場合、数理モデルがグラフの信頼性を左右します。「接触8割減」が必要との科学的根拠は、上掲のグラフ（「提言」図2）でした。グラフの信頼性を検討するには、数理モデルの開示が必要です。

数理モデルを示さなくていいなら、何か科学的根拠のように見えるグラフがあればいいことになってしまいます。それはおかしな考えであるだけでなく、危険な考え方です。

（４）「接触8割減」の数理モデルは示されていない

私は、2020-02-16 の第1回から、2020-06-19 の第17回までの、全ての専門家会議の資料や提言を確認しましたが、「接触8割減」の数理モデルは示されていません。

「接触8割減」の科学的根拠とされるグラフが示された、2020-04-22 専門家会議の資料や「提言」にも数理モデルは示されていません。

また、（専門家会議を引き継いだ）アドバイザリーボードの資料にも「接触8割減」の数理モデルは示されていません。

西浦氏が著書になっている論文にも、「接触8割減」の数理モデルは示されていません。

なお西浦氏は、「42万死亡推計」の数理モデルについては、雑誌記事で周辺事情を説明し、この記事の中で github に置いた数理モデルを示しています。

（５）結論

「接触8割減」が必要とのグラフ（2020-04-22 専門家会議「提言」図2）を描いた数理モデルは、示される必要があるのに、示されていません。

この事実関係は明確で簡潔であり、したがって少なくともこの件に関して西浦氏を「概ね妥当」と肯定的に評価することは出来ません。国民の自由と権利に関わる重大な政策の根拠が示されていないことは、決して小さな問題ではありません。西浦氏の行動を再評価し、今後の政策決定においては透明性と説明責任を重視することが求められます。

更新履歴

2024-06-19
公開。

（１）序論

（２）Google Colab で動作する改変プログラム

(2-1) 作成したプログラムの内容

(2-2) 開示プログラムからの必要最小限の改変

(2-3) プログラムＡ（基準版）が開示プログラムと同様に動作することの確認

（３）開示プログラムは、論文の Figure S5 を再現しない

(3-1) 再現失敗の実証

(3-2) 図3.2 の不一致が私の作図上の不手際ではないことの検証

(3-3) 計算環境への依存性について

（４）デルタ株比率の最適化計算のコスト関数は不適切

(4-1) コスト関数の問題点とその回避策

(4-2) コスト関数の断面の形状 ─ 最適化を誤誘導する仕組み

(4-3) コスト関数が「適切」と示す曲線が白丸のモデルとして適切とは限らない

(4-4) コスト関数を改善する 式(2) 以外の方法

（５）デルタ株比率推定の初期値設定が不適切

(5-1) 単一初期値での最適化は不適切

(5-2) 別初期値でのコストの改善

(5-3) 広範な初期値探索でのコストの大きな改善

（６）結果

（７）考察

（付録Ａ） デルタ株に関する2つの概念

（付録Ｂ） プログラムＡ移動部分の動作確認

（付録Ｃ） 高精度パラメータが必要な理由

（付録Ｄ） 計算環境の検証

（付録Ｅ） 局所極小の実態

更新履歴

（０）本稿公開後に示された、論文の開示情報について（その１）

（１）序論

（２）Figure S5 の赤線は最大値 1 のロジスティック曲線と説明されている

（３）Figure S5 の赤線の最大値は 1 ではない

（４）Figure S5 の赤線のパラメータの推定

（５）（４）節 で推定した曲線と赤線の重ね合わせ（図5.2）

（６）Figure S5 の白丸に適合するロジスティック曲線のパラメータの推定

（７）（６）節 で推定した曲線と白丸の重ね合わせ（図6.1）

（８）最小値0・最大値1に固定したロジスティック曲線による白丸への適合

（９）結果

（１０）考察

（１１）結論

（１２）本稿公開後に示された、論文の開示情報について（その２）

更新履歴

（１）序論

（２）論文 式(2) や 式(3) における新規感染者数の計算

（３）考察：年齢層別の実効再生産数の計算方法

(3-1) 年齢層別の実効再生産数に関係する 式(2) と 式(3)

(3-2) 式(3)説 の検討

(3-2-1) 式(3)説 の詳細

(3-2-2) 式(3)説 の成立に肯定的な事項

(3-2-2-1) 式(3)説 の成立を前提とした言説

(3-2-2-2) 論文の記述

(3-2-3) 式(3)説 の成立に否定的な事項

(3-2-3-1) ワクチンによる免疫の項の問題

(3-2-3-2) 感染による免疫の項の問題

(3-2-3-3) ワクチンによる免疫の項と、感染による免疫の項の問題

(3-3) 式(2)説 について

(3-3-1) 式(2)説 の詳細

(3-3-2) 式(2)説 の成立に肯定的な事項

(3-3-2-1) 論文の記述

(3-3-2-2) 西浦氏の投稿

(3-3-2-3) 同時期に発表された論文が 式(2)説 に該当する方法で計算

(3-3-3) 式(2)説 の成立に否定的な事項

(3-3-3-1) 論文の Figure 1

（４）考察：式(2)説 と 式(3)説 どちらが有力なのか

（５）考察：式(2)説 ならば Figure 1 の fit は当然

（６）考察：式(2)説 の場合の反実仮想シナリオ計算への影響

（７）結論

参考文献

修正履歴

（１）序論

（２）論文におけるワクチンの効果は、（発症予防効果ではなく）感染予防効果

（３）論文がワクチンの効果の根拠とした2つの論文

(3-1) Sci Rep 2023 論文におけるワクチン効果の記述

(3-2) [Goldberg 2021] が調べているワクチンの効果

(3-3) [Tartof 2021] が調べているワクチンの効果

（４）考察

（５）結論

参考文献

修正履歴

（１）序論

（２）雨と傘の例え

(2-1) 雨と傘の例えの対応表と Sci Rep 2023 論文のシナリオ

(4-4) コスト関数を改善する式(2) 以外の方法

（付録Ａ）デルタ株に関する2つの概念

（付録Ｂ）プログラムＡ移動部分の動作確認

（付録Ｃ）高精度パラメータが必要な理由

（付録Ｄ）計算環境の検証

（付録Ｅ）局所極小の実態

（５）（４）節で推定した曲線と赤線の重ね合わせ（図5.2）

（７）（６）節で推定した曲線と白丸の重ね合わせ（図6.1）

（２）論文式(2) や式(3) における新規感染者数の計算

(3-1) 年齢層別の実効再生産数に関係する式(2) と式(3)

(3-2) 式(3)説の検討

(3-2-1) 式(3)説の詳細

(3-2-2) 式(3)説の成立に肯定的な事項

(3-2-2-1) 式(3)説の成立を前提とした言説

(3-2-3) 式(3)説の成立に否定的な事項

(3-3) 式(2)説について

(3-3-1) 式(2)説の詳細

(3-3-2) 式(2)説の成立に肯定的な事項

(3-3-2-3) 同時期に発表された論文が式(2)説に該当する方法で計算

(3-3-3) 式(2)説の成立に否定的な事項

（４）考察：式(2)説と式(3)説どちらが有力なのか

（５）考察：式(2)説ならば Figure 1 の fit は当然

（６）考察：式(2)説の場合の反実仮想シナリオ計算への影響

(2-2-1) 接触削減の評価方法の大混乱概要

(2-2-2) 接触削減の評価方法の大混乱詳細