Гипотеза Коллатца

Последовательности для всех нечётных чисел от 1 до 49 включительно (кроме чисел 27, 31, 41, 47). Чётные числа в последовательности опущены

Гипотеза Ко́ллатца — одна из нерешённых проблем математики: верно ли, что последовательность чисел, строящаяся от произвольного натурального $n_{0}$, каждое $(i+1)$-е число в которой равно $3n_{i}+1$, если $n_{i}$ — нечётное, и $n_{i}/2$, если $n_{i}$ — чётное, рано или поздно вырождается в единицу. Такие последовательности называются сиракузскими, а гипотеза иногда фигурирует как под наименованием «сираку́зская проблема».

Названа по имени немецкого математика Лотара Коллатца, сформулировавшего похожую задачу 1 июля 1932 года.

Последовательности для первых чисел:

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
	1	10	2	16	3	22	4	28	5	34	6	40	7	46	8
		5	1	8	10	11	2	14	16	17	3	20	22	23	4
		16		4	5	34	1	7	8	52	10	10	11	70	2
		8		2	16	17		22	4	26	5	5	34	35	1
		4		1	8	52		11	2	13	16	16	17	106
		2			4	26		34	1	40	8	8	52	53
		1			2	13		17		20	4	4	26	160
					1	40		52		10	2	2	13	80
						20		26		5	1	1	40	40
						10		13		16			20	20
						5		40		8			10	10
						16		20		4			5	5
						8		10		2			16	16
						4		5		1			8	8
						2		16					4	4
						1		8					2	2
								4					1	1
								2
								1

График последовательности для числа 27

При $n=27$ последовательность состоит из 111 членов до первой единицы, достигая в пике значения 9232.

Благодаря элементарности формулировки проблема снискала широкую известность, фигурировала во множестве научно-популярных публикаций, создано множество визуализаций для умозрительного поиска закономерностей. Запущено несколько проектов добровольных вычислений по проверке гипотезы: в августе 2009 года — на платформе BOINC (с поддержкой GPGPU), в августе 2017 года — в рамках проекта «yoyo@home».

В последние годы^{[уточнить]} проверены все натуральные числа до 3×10²⁰, и каждое из них продемонстрировало соответствие гипотезе Коллатца.

Визуализации

• 
  Направленный график, показывающий орбиты первых 1000 чисел.
• 
  Ось $x$ представляет начальное число, ось $y$ — наибольшее число, достигнутое в цепочке до 1. Этот график показывает ограниченность оси y: некоторые значения $x$ дают промежуточные значения, достигающие 2,7e7 (для $x=9663$)
• 
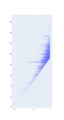
  График в логарифмическом масштабе; первая жирная линия в середине графика соответствует вершине в точке 27, которая достигает максимума в точке 9232.
• 
  Дерево всех чисел, имеющих меньше 20 шагов.
• 
  Количество итераций, необходимое для достижения единицы для первых 100 миллионов чисел.
• 
  Пути по гипотезе Коллатца для 5000 случайных начальных точек меньше 1 миллиона.

Литература

• Хэйес, Брайан. Взлёты и падения чисел-градин // В мире науки (Scientific American, издание на русском языке). — 1984. — № 3. — С. 102—107.
• Стюарт, Иэн. Величайшие математические задачи. — М.: Альпина нон-фикшн, 2015. — 460 с. — ISBN 978-5-91671-318-3.
• Jeff Lagarias. The 3x+1 problem and its generalizations (англ.) // American Mathematical Monthly. — 1985. — Vol. 92. — P. 3—23.

Ссылки

• последовательность A014682 в OEIS.
• Самая простая нерешённая задача — гипотеза Коллатца (YOUTUBE)  (рус.) (Видео). www.youtube.com. Дата обращения: 2 ноября 2022. Архивировано 2 ноября 2022 года.
• Das Collatz-Problem интерактивные скрипты Юргена Денкерта для решения (3n+1)- и (3n−1)-задач, создаёт последовательность для чисел любой длины, также выдаёт статистику последовательности.
• Collatz Conjecture Архивная копия от 4 декабря 2017 на Wayback Machine — проект распределённых вычислений на платформе BOINC по проверке гипотезы Коллатца на больших числах.
• On the 3x + 1 problem Архивная копия от 14 декабря 2013 на Wayback Machine — проект распределённых вычислений, основанный Эриком Рузендалем (Eric Roosendaal), по проверке гипотезы Коллатца на больших числах.
• Аналитический подход к проблеме Коллатца Архивная копия от 20 марта 2013 на Wayback Machine. (англ.)
• Реализация сиракузской последовательности на разных языках программирования Архивная копия от 4 апреля 2018 на Wayback Machine (на сайте Rosetta Code).
• Collatz conjecture A.A Durmagambetov, A. A Durmagambetova. https://www.researchgate.net/publication/359521315_Collatz_conjecture