見出し画像

UEでポータルをフルスクラッチで作る（Off Axis Projection Matrix入門）

Yohei Kajiwara

概要

Party内のテックチーム「PY」のテック記事連載です。
前回タケルさんの記事でCES2024で作った「Holo Window」について触れていたので、そのコアとなる仕組みに関してコードを見せつつご紹介しようと思います。
デジタルツイン側の世界を覗き込める、「ポータル出現」的な演出をやるための技術的なバックグラウンドと、UEでの実装例です。

たとえばこういうことができます。（2020年とかのネタなんでだいぶ古いですが、、、）

コード全容

参考までに

  • UEのプラグインです

  • だいぶ前に作ったやつなんでUE4って名前ですが、UE5でも動きます（5.5でも動作確認済み）

  • 雑なコードなので、あくまで参考程度としてどうぞ

  • この記事用にPublicにしてみましたが、様子見てまたPrivateに戻すかも

ポータルとは

さて、みなさんポータル表現は好きでしょうか？
いわゆる「空間に空いた異世界への覗き窓」ってやつですね。
最近のゲームでは普通にあるし、Apple Vision Proでもそういう機能が普通に実装されてるので馴染みのある方も多いかと思います。

ちょっと昔は機能として提供されている訳ではなかったので、自分でイチから実装する必要がありました。
僕の場合はプラグインなどでモジュール化しておくのが好きなので、だいぶ昔にUE用のプラグインとして実装したものを案件に応じて改造したりして使っています。

今回はそれを使ったプロダクトと合わせて、理論と実装の部分をご紹介します。

Holo Windowとは

透過有機ELディスプレイ越しにXR表現が可能な、裸眼XRシステムです。
仕組みとしては単純で、

  • 実際の環境と全く同一寸法のデジタルツインをゲームエンジン（UE）内に作成

  • デジテルツイン内に、透過有機ELディスプレイと全く同じ位置に、ポータルを設置

  • 鑑賞者の眼球の位置をトラッキング

  • 眼球の位置にあわせてポータルに写る内容を生成

  • 透過有機ELディスプレイに描画

って感じです。
↓な感じで実際のオブジェクトにCGを重ねることが可能になります。

ポータル越しに、現実とデジタルツインが重なり合っているって感じの表現がリアルタイムで可能になります。
最近の眼球トラッキングはAIの発展もあり遅延がかなり少なくなってきたので、体験としてもかなり面白い感じになっています。
何より、裸眼でXR的なことができるので気軽で良いですね。

ポータルはどんな原理でできているか？

さて、そもそもポータルを実現するにはどうしたら良いのか？
ちょっと実際の空間で考えてみましょう。

空間にある窓に映る景色

とある空間に浮かんだ窓があるとして、そこに写る（描画されている）のはどんな像でしょうか？
まず単純な例から順番に考えていきます。

1. 見ている方向（軸）と窓の中心が一致しているパターン

視線と同軸にある窓から見える景色

CGやゲームエンジンとかを触る人にはこれが一番お馴染みかと思います。
要は自分のビュー＝カメラのビューっていうパターンですね。

窓の中心軸と、見ている軸が同一

ただのカメラとの違いは、

  • 画角はその窓のサイズと距離で決まる

  • カメラの縦横比は窓の縦横比と同様

ってことかと思います。
これは実装も簡単そうですね。窓の中心への距離・窓の長辺が分かれば画角が分かりますし、縦横比も簡単です。

え、窓が傾いていたらどうなるの？

ちょっと例外的なパターンも思い浮かぶかと思います。
軸は同一なんだけど、窓が傾いてたらどうなのかしら？ってパターンです。
これ、実際に自分で適当な枠を用意して試してみてもらうと良いのですが、実は上のパターンの派生で処理できます。
結論から言うと、単に窓のサイズが変わるだけで良いですよね。

窓が傾いていても、軸が同じなら正面を向いたものとして計算できる

とりわけゲームエンジン内のカメラはレンズ歪みがないので、理論上は距離による像の歪みがないため、窓のサイズが変わったとして描画するだけで成立します。
実際に、自分の目の前にフレームを作ってみて、それを傾けたらどうなるか？やってみてください。

Projection Matrix（投影行列）

さて、ここまでで、
、、、っていうかこれ普通のゲーム内のカメラの設定じゃね？
って思ったあなたは正解です。

「空間内における、ある枠内に描画される像を計算する」というタスクで、これはゲームエンジン内のカメラが行なっている計算と同様です。

「Projection Matrix（投影行列）」という言葉、聞いたことがあるかと思います。
Projection Matrix（投影行列）とは、3D空間（カメラ空間）上の点を、レンダリングや画像表示のために2Dの投影面（スクリーン空間）へ写す変換を担う行列です。

ここでは、窓の軸と同じ軸（On Axis）からの計算なので、
「On Axis Projection Matrix」となります。
また、2Dの投影面＝窓って感じなので、まさしくこのProjection Matrixを計算するってことと同一ですね！
そしてこれは普通にゲームエンジンのカメラがやってる内容なので、そもそも実装の必要すらありません。

2. 見ている方向（軸）と窓の中心が一致していないパターン

自分の横にある窓からはどのような景色が見えるだろうか

では、見ている方向と窓の中心が一致していないとどうでしょうか？
窓の中心軸での回転は計算にさほど影響しないことがここまでで分かっているので、観察者と平行においてあるとします。

窓の軸と、見ている軸がずれている

これも、実際に自分でフレームを目の前に置いてみて、もしくは窓の前に立ってみて、どんなビューが見えるかを体感してみましょう。
ポイントは、窓の方を向いたり顔を少し動かしても窓の中の景色が変わらないってことです。
要は、みている方向ではなく、目の位置と窓の位置関係が重要ということですね。

その上で、これはどう計算したら良いでしょうか？
ここで出てくるのが、「Off Axis Projection Matrix（非同軸投影行列）」です。

On Axisの場合、軸が同じ。という特殊な状況でした。顔の真正面にずっと窓がある状態。
Off Axisはこれをより一般化したものです。

ちょっと行列（Matrixは行列のこと）とか出てくるので、苦手な人はさーっとスクロールしつつ、すっ飛ばしてコードのとこを見てください！
あと、長くなりすぎるので、これらの行列の求め方は省略します！調べるとめちゃくちゃ面白いので是非調べてみてください。

Projection Matrix（同軸投影行列）をみてみよう

まず、同軸のProjection Matrixはどんなものか見てみましょう！
ここまではポータルを「窓」として表現してきましたが、実装の話になってきたので一般的な「スクリーン（投影面）」という言葉に言い換えます。

スクリーン（投影面）の中心軸がカメラの正面を向き、上下左右対称なフラスタムを設定すると、行列はこんな感じになります。

$$
P_{\text{on-axis}} = \begin{pmatrix}
\frac{1}{a \tan(\frac{\theta}{2})} & 0 & 0 & 0 \\
0 & \frac{1}{\tan(\frac{\theta}{2})} & 0 & 0 \\
0 & 0 & -\frac{f+n}{f-n} & -\frac{2fn}{f-n} \\
0 & 0 & -1 & 0
\end{pmatrix}
$$

• a は画面のアスペクト比（幅÷高さ）
• \theta は垂直視野角（FOV）
• n は近クリップ面の距離 (near)
• f は遠クリップ面の距離 (far)

なんだかわけわかめって感じになりそうですが、図にしてみると分かりやすいかと思います。

”The Perspective and Orthographic Projection Matrix”より抜粋

また、たくさん変数があるように見えますが、要するに
FOV, アスペクト比
が分かればそのスクリーン（近クリップ面）に描画するものが決められるってのがわかると思います。
実際に実装する際は、これらの変数を計算し、ゲームエンジンのカメラのProjection Matrixとして上書いてやればいいって感じです。（まぁデフォで計算されていますが）

Off Axis Projection Matrix（非同軸投影行列）をみてみよう

ではOff Axis Projection Matrixはどんな様相をみせるのか。
こんな感じです。

$$
P_\text{off-axis} = \begin{pmatrix}
\dfrac{2n}{r-l} & 0 & \dfrac{r+l}{r-l} & 0 \\
0 & \dfrac{2n}{t-b} & \dfrac{t+b}{t-b} & 0 \\
0 & 0 & -\dfrac{f+n}{f-n} & -\dfrac{2fn}{f-n} \\
0 & 0 & -1 & 0
\end{pmatrix}
$$

あれ？そんなに複雑でもない？
一見すると普通のProjection Matrixによく似ていますね。
違いは変数たちです。

• l, r: 近クリップ面における左右の端の位置
• b, t : 近クリップ面における下端・上端の位置
• n, f はOn Axisと同様

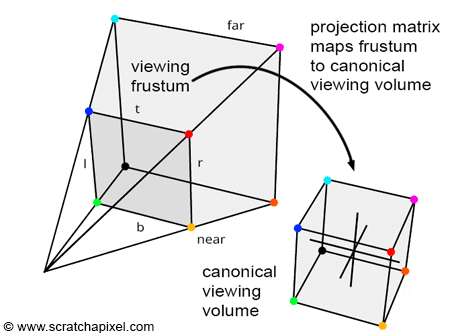
”The Perspective and Orthographic Projection Matrix”より抜粋

FOVやアスペクト比の変わりに、スクリーンの位置の情報が変数としてあります。
ちなみに、スクリーンを同軸にするように配置して、この変数にはめれば、実質On Axisと同じ内容になります。要はOn Axisのより一般化された形であるのがわかるかと思います。

要は、スクリーンの位置さえ分かれば、それを元にこの行列は作れると。
そして、それを使ってゲームエンジンのカメラのProjection Matrixを上書いちゃえば良いっていうノリがわかるかと思います。

UEで実装していこう

＊全容はGithubのレポジトリをみてください

さて、UEで実装するにあたり、デフォルトのカメラのProjection Matrixを書き換えるので、何がしかのカメラのクラスを継承したクラスを作成した方が良さそうです。
ってことで、今回はSceneCapture2Dのカメラを継承して、そのカメラの出力をポータル（近クリップ面）にするようにしましょう。
ついでにターゲットとなるスクリーンをコンポーネントとして作っておけば、XRをやる際にも扱いやすくなります。
このスクリーンの位置と、カメラの位置を使ってOff Axis Projection Matrixを作成し、カメラのProjection Matrixを上書きするような設計にしてみましょう。

ここまでを踏まえると、以下の情報を捌いていけば良さそうです。

  • ポータルを描画するスクリーンの左右、上下の端の情報

また、スクリーンがどっち向いてるか？も大事なので、上記の情報で向きがわかるような作りが良さそう。
そうなると、4点ではなく3点の情報で良さそうですね。

球の名称をそれぞれ、スクリーン左上：pc、左下：pa、右下：pbとする

まずターゲットとなるスクリーンを設置できるように、Actorとして左上下、右下に目印として球を付けたスクリーンを用意します。
BP_OffAxisProjection_TargetScreen的な名前のBPクラスです。
これをSceneCapture2Dを継承したC++クラス（BP_OffAxisProjectionSceneCapture2Dとでもしておきましょう）に参照させてやることで、スクリーンの情報を取得できるようにしましょう。

カメラがBP_OffAxisProjectionSceneCapture2D

さて、このスクリーンを設置し、参照すると情報を取得できます。
ということで、まずこんな定数を作ります。

float OffAxisNearPlane = .1f;
float OffAxisFarPlane = 10000.f;

FVector pa = FVector(80.f, 40.f, 0.f);
FVector pb = FVector(-80.f, 40.f, 0.f);
FVector pc = FVector(80.f, 130.f, 0.f);
FVector pe = FVector::ZeroVector;

で、これらの情報をアップデートするためにこんな感じの関数を作ります。

UFUNCTION(BlueprintCallable, meta = (DisplayName = "SetTargetQuadPoints", Keywords = "OffAxisProjection SetTargetQuadPoints"), Category = "OffAxisProjection SceneCapture2D")
		void SetTargetQuadPoints(FVector _pa, FVector _pb, FVector _pc);

で、これらの情報を元にProjection Matrixを作成する関数を用意。
この引数のeyeRelativePositionは、カメラ空間でのスクリーンの位置を渡す想定です。（後ほどこれも実装しましょう）

FMatrix GenerateOffAxisMatrix(FVector _eyeRelativePositon);

さて、一旦これらの中身を実装してみましょう。
まずスクリーンの情報の更新。これは簡単ですね。

void AOffAxisProjectionSceneCapture2D::SetTargetQuadPoints(FVector _pa, FVector _pb, FVector _pc)
{
	pa = FVector(_pa.Y, _pa.Z, _pa.X);
	pb = FVector(_pb.Y, _pb.Z, _pb.X);
	pc = FVector(_pc.Y, _pc.Z, _pc.X);
}

次に、Off Axis Projection Matrixの作成

FMatrix AOffAxisProjectionSceneCapture2D::GenerateOffAxisMatrix(FVector _eyeRelativePosition)
{
	FMatrix result;

	float l, r, b, t, n, f, nd;

	n = OffAxisNearPlane;
	f = OffAxisFarPlane;

	//this is analog to: http://csc.lsu.edu/~kooima/articles/genperspective/
	//Careful: coordinate system! y-up, x-right (UE4 uses inverted LHS)

	//pa = lower left, pb = lower right, pc = upper left, eye pos
	pe = FVector(_eyeRelativePosition.X, _eyeRelativePosition.Y, _eyeRelativePosition.Z);

	// Compute the screen corner vectors.
	FVector va, vb, vc;
	va = pa - pe;
	vb = pb - pe;
	vc = pc - pe;

	// Compute an orthonormal basis for the screen.
	FVector vr, vu, vn;
	vr = pb - pa;
	vr.Normalize();
	vu = pc - pa;
	vu.Normalize();
	vn = -FVector::CrossProduct(vr, vu);
	vn.Normalize();

	// Find the distance from the eye to screen plane.
	float d = -FVector::DotProduct(va, vn);

	nd = n / d;

	// Find the extent of the perpendicular projection.
	l = FVector::DotProduct(vr, va) * nd;
	r = FVector::DotProduct(vr, vb) * nd;
	b = FVector::DotProduct(vu, va) * nd;
	t = FVector::DotProduct(vu, vc) * nd;

	// Load the perpendicular projection.
	result = FrustumMatrix(l, r, b, t, n, f);

	//Move the apex of the frustum to the origin.
	result = FTranslationMatrix(-pe) * result;

	//scales matrix for UE4 and RHI
	result *= 1.0f / result.M[0][0];

	result.M[2][2] = 0.f; //?
	result.M[3][2] = n; //?

	return result;
}

やっていることは比較的シンプルで、前述のl, r, b, tおよび、近クリップ面nと遠クリップ面fを求め、行列を作っているって感じです。
行列自体は、FrustumMatrixという関数を別途作り、ここで作成。
その後、UEのご都合に合わせて少し変換などかけてあげれば完成です。
一応FrustrumMatrixはこんな感じ。単に行列の形式に整形するだけですね。

FMatrix AOffAxisProjectionSceneCapture2D::FrustumMatrix(float left, float right, float bottom, float top, float nearVal, float farVal)
{
	//column-major order
	FMatrix Result;
	Result.SetIdentity();
	Result.M[0][0] = (2.0f * nearVal) / (right - left);
	Result.M[1][1] = (2.0f * nearVal) / (top - bottom);
	Result.M[2][0] = -(right + left) / (right - left);
	Result.M[2][1] = -(top + bottom) / (top - bottom);
	Result.M[2][2] = (farVal) / (farVal - nearVal);
	Result.M[2][3] = 1.0f;
	Result.M[3][2] = -(farVal * nearVal) / (farVal - nearVal);
	Result.M[3][3] = 0.0f;

	return Result;
}

さて、それではカメラ本体のProjection Matrixを更新しましょう。
こんな関数にしてみました。

void AOffAxisProjectionSceneCapture2D::UpdateProjectionMatrix_Internal(USceneCaptureComponent2D* captureComponent2D, FMatrix OffAxisMatrix)
{
	FMatrix stereoProjectionMatrix = OffAxisMatrix;

	FMatrix axisChanger; //rotates everything to UE4 coordinate system.
	axisChanger.SetIdentity();
	axisChanger.M[0][0] = 0.0f;
	axisChanger.M[1][1] = 0.0f;
	axisChanger.M[2][2] = 0.0f;
	axisChanger.M[0][2] = 1.0f;
	axisChanger.M[1][0] = 1.0f;
	axisChanger.M[2][1] = 1.0f;

	//View->ViewRotation = s_ViewRotation;
	FMatrix tmpMat = axisChanger * stereoProjectionMatrix;
	GEngine->AddOnScreenDebugMessage(11, 4, FColor::Red, FString::Printf(TEXT("tmpMat SC2D: %s"), *tmpMat.ToString()));

	FMatrix calcedMatrix = GetProjectionMatrix(captureComponent2D);
	//GEngine->AddOnScreenDebugMessage(16, 4, FColor::Red, FString::Printf(TEXT("calced SC2D: %s"), *calcedMatrix.ToString()));

	if (captureComponent2D)
	{
		const FVector curLocation = GetActorLocation();
		FMatrix ViewMatrix = FMatrix(
			FPlane(0, 1, 0, 0),
			FPlane(0, 0, 1, 0),
			FPlane(1, 0, 0, 0),
			FPlane(curLocation.X, curLocation.Y, curLocation.Z, 1)
		);

		FMatrix finalMat = ViewMatrix * tmpMat;
		GEngine->AddOnScreenDebugMessage(16, 4, FColor::Red, FString::Printf(TEXT("Transform inv SC2D: %s"), *ViewMatrix.ToString()));
		GEngine->AddOnScreenDebugMessage(18, 4, FColor::Red, FString::Printf(TEXT("Result SC2D: %s"), *finalMat.ToString()));

		captureComponent2D->CustomProjectionMatrix = finalMat;
	}
}

引数は上書きされるやつ＝USceneCaptureComponent2Dと、作成したOffAxisProjectionMatrixです。
UE用の座標系に軸系の変換などをしていますが、基本的にはUSceneCaptureComponent2Dから引っ張ってきたProjectionMatrixを元にして、先ほど生成したOffAxisProjectionMatrixを適用します。

あとは、Tickのタイミングでこれを行うようにすれば、カメラの位置に応じて随時更新してくれます。（Githubのコードの方は、TickによるUpdateをBlueprint側に移してます）

void AOffAxisProjectionSceneCapture2D::Tick(float DeltaSeconds)
{
	Super::Tick(DeltaSeconds);

	USceneCaptureComponent2D* captureComponent2D = GetCaptureComponent2D();
	if (captureComponent2D)
	{
		FVector pos = GetActorLocation();
		GEngine->AddOnScreenDebugMessage(10, 1, FColor::Green, FString::Printf(TEXT("SceneCapture2d pos: (%f, %f, %f)"), pos.X, pos.Y, pos.Z));
		eyePosition.X = pos.Y;
		eyePosition.Y = pos.Z;
		eyePosition.Z = pos.X;
		UpdateProjectionMatrix_Internal(captureComponent2D, GenerateOffAxisMatrix(eyePosition));
	}
}

実際に使ってみよう

プラグインのコンテンツを表示すると、こんな感じにコンテンツが入ってる

  • カメラとスクリーンを置き、

  • カメラにスクリーンのクラスを参照させ、

  • カメラ（SceneCapture2D）の出力先として適当なRenderTextureと、そのTextureからMaterialを作成、

  • Materialをスクリーンのプレーンに張り付ける

以上！ってかんじで、簡単にOffAxisProjectionMatrixを使えます。

これをXRにする場合は、カメラの位置をユーザーの目の位置、スクリーンの位置を実際の透過スクリーンの位置にしてやるだけでOKです。簡単。
もちろんゲーム内でも使えますが、あんましパフォーマンスのことは考えてない、あくまで基本的な実装なのでその辺は適当にプロジェクトに応じてカスタマイズしましょう。
中身を自作すると、その自由度があります。

最後に

この考え方は、UnityでもTouchdesignerでも使えます。どちらもProjectionMatrixをカスタムで書き換えることは可能なので、たとえば間違った実装をするとすごくノイジーな表現になったりしますし、特にTouchdesignerでこういうことをしてる事例をあまり見かけないのでぜひトライしてみてください！
DirectXとOpenGLや座標系の違いがあるのでそのままではうまくいかないと思いますが、理屈は一緒です。

本記事を執筆ついでに動作確認したUE5.5のSampleプロジェクトのDLリンク貼っておきます。興味のある方は適当に触ってみてください。
https://www.dropbox.com/scl/fi/lpjn2lqgcu8me5d2sz51e/OffAxisPrj_Sample.zip?rlkey=adfz7lefkv591sf4jict32pby&dl=0

いいなと思ったら応援しよう！